前回はARモデルで乗客数を予測してみました。
精度は定量的に測ってはいませんが、正解データと比較してみると非常に良さそうに思えました。
MAやARMAモデルなど試してみたいところですが、いきなりSARIMAモデルを試してみようと思います。
引き続き、seabornを使いますのでインストールしていない方は pip install seabornでインストールしてください。
seabornのflightデータの確認
flightsデータの中身をビジュアル化しています。確認したい方は下記から参照ください。

USの国際線乗客数をSARIMAモデルで予想する
SARIMAモデルを適用する前までのデータ加工の部分はARモデルの記事と共通になります。

試行錯誤している部分などもARモデルの記事では記載していますが、本記事では最低限必要な部分のみ記載します。
# 描画設定
from IPython.display import HTML
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12 # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12 # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18 # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8 # 画像サイズの変更(inch)データの読み込みとデータ加工
import pandas as pd
# データの読み込み (既に読み込み済みだが、読みやすさのためもう一度実行する)
flights = sns.load_dataset("flights")
# 日付変換用カラムの作成
flights["date"] = flights.year.astype('str') + "-" + flights.month.astype('str')
# 日付カラムの作成
flights["ds"] = pd.to_datetime(flights["date"], format="%Y-%b")
# datetimeをindexに設定、目的変数の型をfloat64に変換
flights = flights.set_index('ds').astype({'passengers': 'float64'}).drop(["date"], axis=1)
# 日付の間隔をasfreqメソッドで変更する
flights = flights.asfreq('MS')非定常過程のデータを定常過程のデータに変換する (log(現在値) - 移動平均値)
対数変換した乗客数とその移動平均値を利用してデータの変換します。
# データの変換
flights_log_ma12 = np.log(flights[["passengers"]]).copy() # 対数変換したpassengers
flights_log_ma12["passengers_original"] = flights[["passengers"]].copy() # 対数変換する前のpassengers
flights_log_ma12["passengers_ma"] = flights_log_ma12[["passengers"]].rolling(window=12).mean() # 対数変換済みpassengersの移動平均
flights_log_ma12["passengers_smoothed"] = flights_log_ma12["passengers"] - flights_log_ma12["passengers_ma"] # 対数変換済みpassengers - 対数変換済みpassengersの移動平均
flights_log_ma12 = flights_log_ma12.dropna() # 移動平均を計算するときに最初の12件はNAになるので除外# 上から5件を確認
flights_log_ma12.head()
passengers passengers_ma passengers_smoothed ds 1949-12-01 4.770685 4.836178 -0.065494 1950-01-01 4.744932 4.838381 -0.093449 1950-02-01 4.836282 4.843848 -0.007566 1950-03-01 4.948760 4.849344 0.099416 1950-04-01 4.905275 4.853133 0.052142
flights_log_ma12.passengers_smoothed.plot()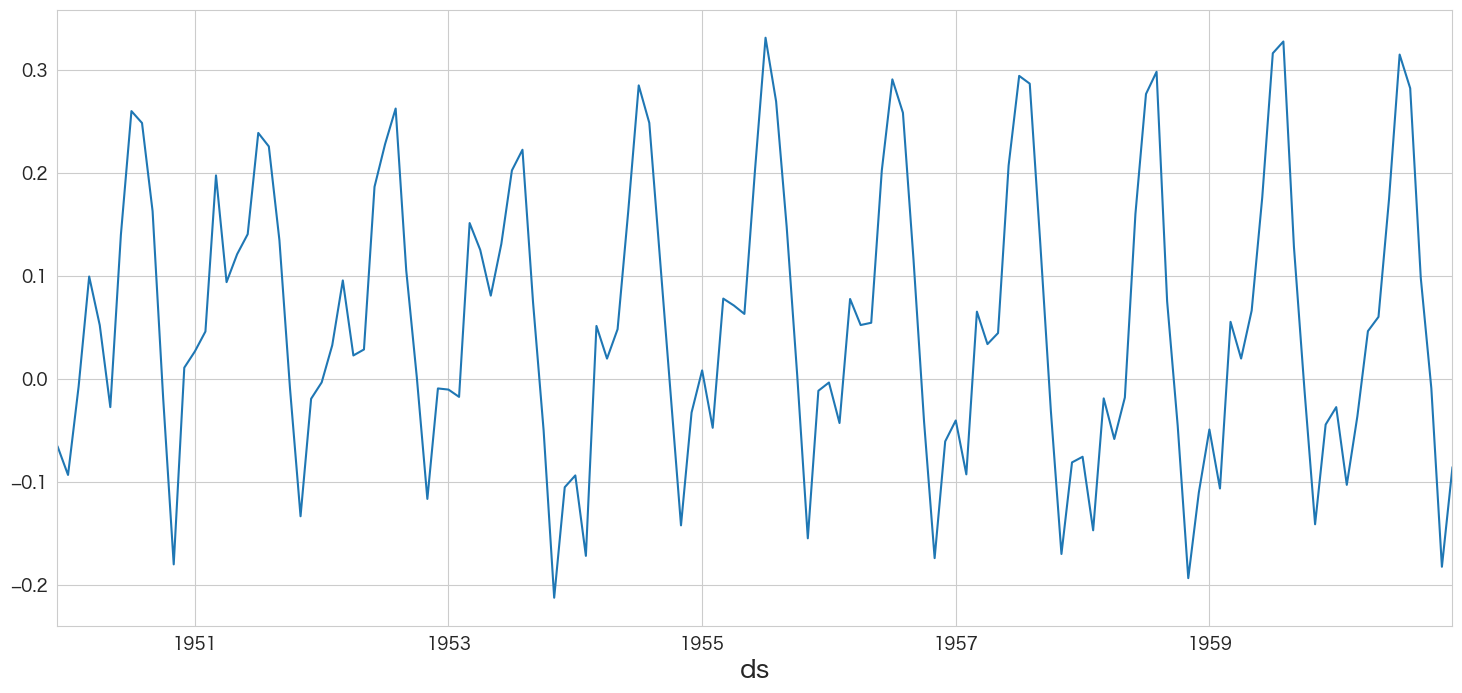
定常過程のようなデータになりました。
トレンドの検定
# トレンドの検定
import pymannkendall as mk
mk.original_test(flights_log_ma12["passengers_smoothed"])Mann_Kendall_Test(trend='no trend', h=False, p=0.34948618250936936, z=-0.9355863941191324, Tau=-0.05491000227842333, s=-482.0, var_s=264315.3333333333, slope=-0.0003134931759312842, intercept=0.06665537246320051)
定常性の検定
# 定常性の検定
from statsmodels.tsa.stattools import adfuller
# 検定結果を見やすく加工(トレンドが存在しないので、regression='c'に設定した)
result = adfuller(flights_log_ma12["passengers_smoothed"],regression='c')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result検定統計量 -3.162908 P値 0.022235 #ラグ数 13.000000 #観測数 119.000000 臨界値 (有意水準:1%) -3.486535 臨界値 (有意水準:5%) -2.886151 臨界値 (有意水準:10%) -2.579896 dtype: float64
P値 < 0.05なので帰無仮説が棄却され対立仮説である「単位根がない」が採用されます。単位根がないので弱定常過程であるとみなします。
時系列成分の分解
# 時系列成分の分解
from statsmodels.tsa.seasonal import STL
res = STL(flights_log_ma12["passengers_smoothed"]).fit()
res.plot()
plt.show()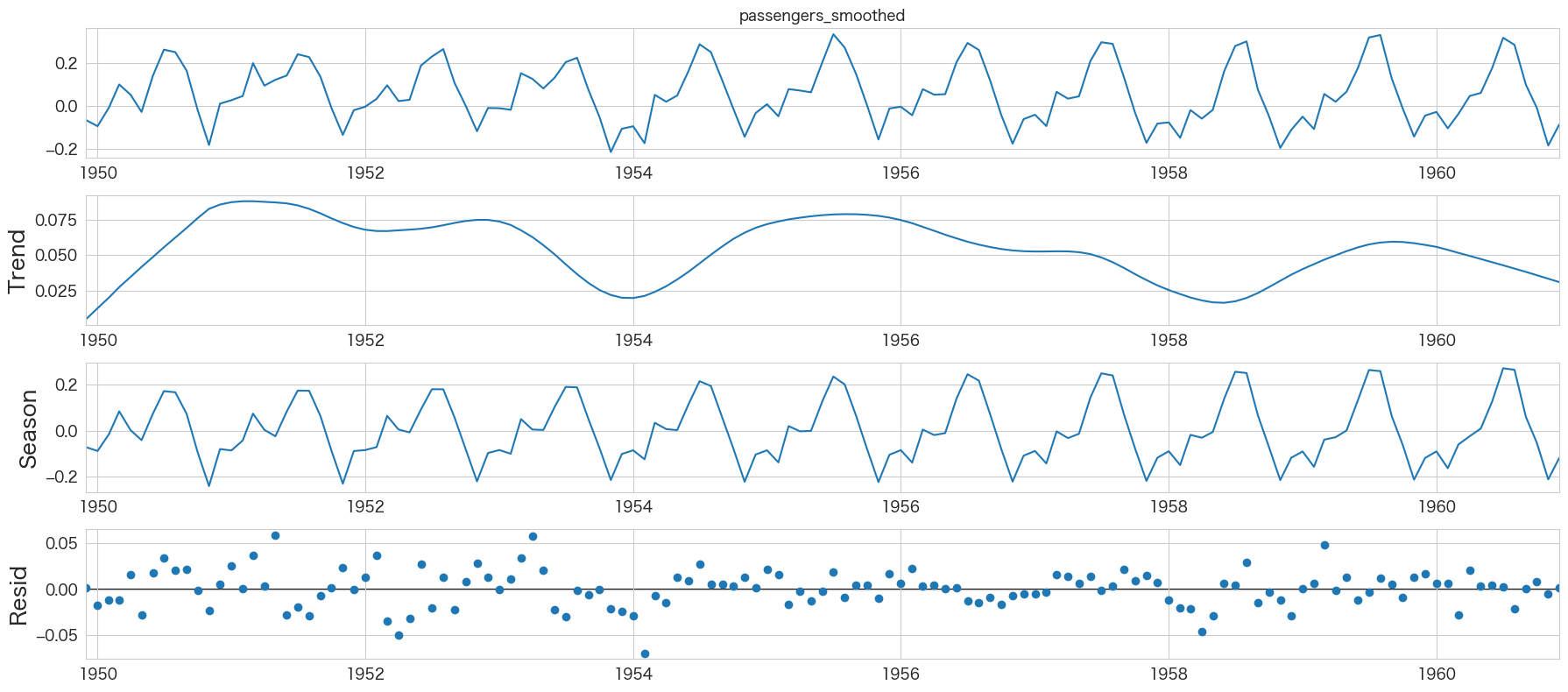
周期性があるのが分かります。
自己相関係数の確認
# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np
fig, ax = plt.subplots(figsize=(16,8))
plot_acf(flights_log_ma12["passengers_smoothed"], lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()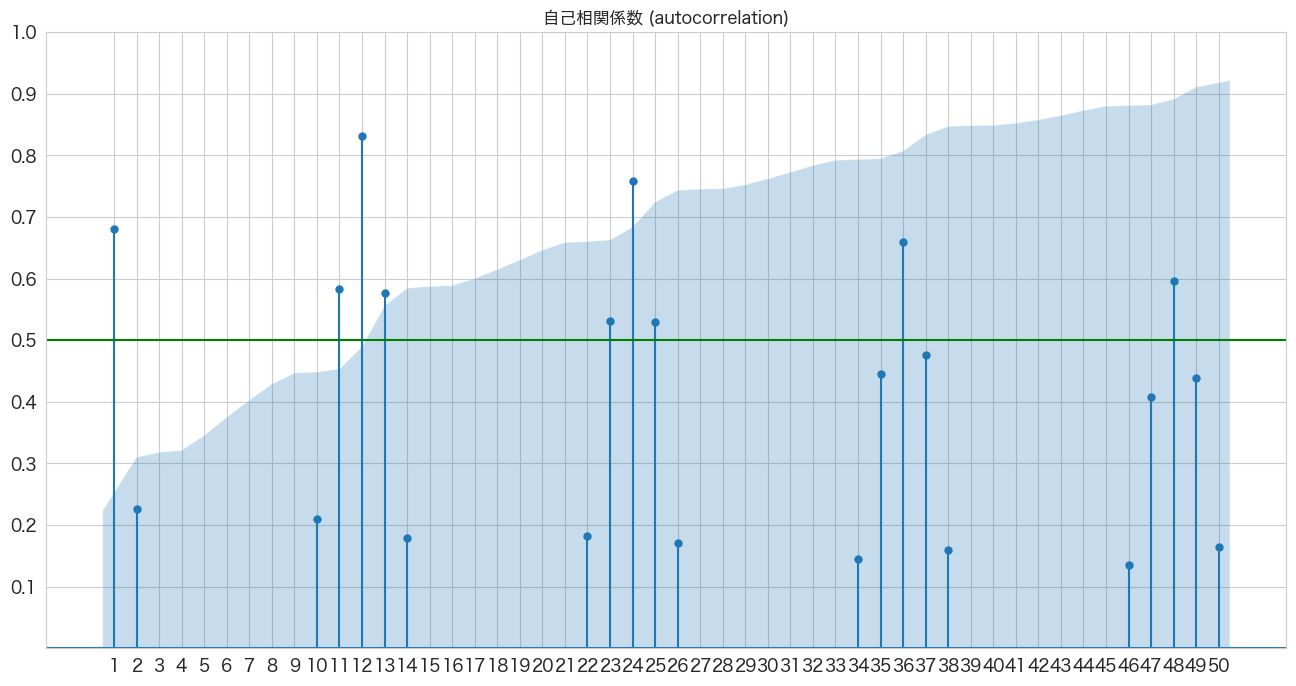
1年ごとの周期性がありそうですね
偏自己相関係数の確認
# 偏自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_pacf
import numpy as np
fig, ax = plt.subplots(figsize=(16,8))
plot_pacf(flights_log_ma12["passengers_smoothed"], lags=50, zero=False, title="偏自己相関係数 (partial autocorrelation)", method=('ywm'), ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.axhline(y=0.5, color="green")
plt.show()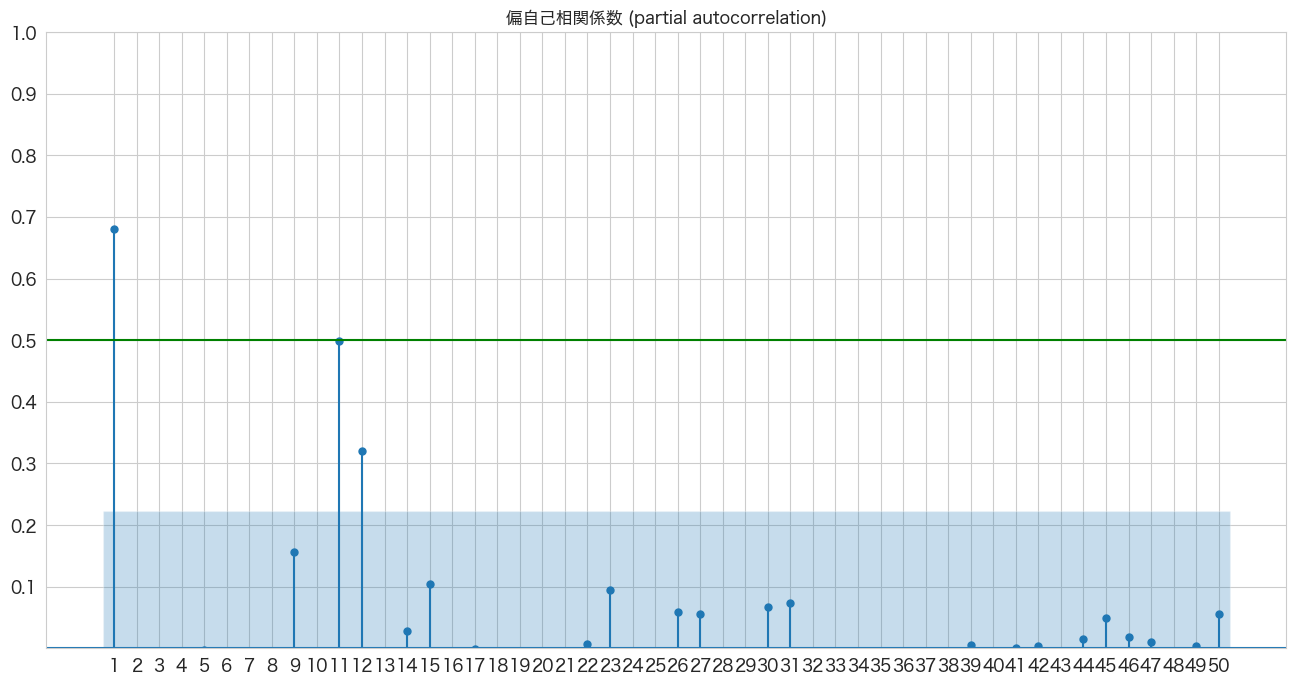
AR(1)、AR(11、AR(12)らへんが青いエリア外(自己相関は0ではない)にあるようです。
SARIMAモデルの作成
シンプルなSARIMAモデルを作成した例はこちらにあります。
今回は最初から最適なパラメータを探索するauto-sarimaでモデリングしちゃいます。
pmdarimaというライブラリを使いますので、事前にpip install pmdarimaが必要です。
訓練データとテストデータに分割
# 訓練用とテスト用に分ける
df = flights_log_ma12.iloc[:-12].copy() # 1949-12 ~ 1959-12
df_test = flights_log_ma12.iloc[-12:].copy() # 1960-01 ~ 1960-12p値=0.0で有意差あり
有意差ありなのでAR(2)の方が良いモデルという結果になりました。
このように対数尤度比検定を次数を変えたモデルを適用し、最適なARモデルを探索していこうと思います。
(オプション) 階差の最適な数値を求める
SARIMAモデルの「I」の部分の値を求めます。
下記SARIMAモデルのパラメータで言うと、「d」の部分になります。
SARIMA( p,d,q )( P,D,Q )[m]
ちなみに、p,d,qだけだとARIMAモデルになりますが、ARIMAモデルに( P,D,Q )[m]を追加したものがSARIMAモデルになります。
各パラメータの意味は下記になります。
p: The order of the auto-regressive (AR) model.
d: The degree of differencing.
q: The order of the moving average (MA) model.
P: The order of the seasonal component for the auto-regressive (AR) model.
D: The integration order of the seasonal process.
Q: The order of the seasonal component of the moving average (MA) model.
m: The number of observations per seasonal cycle. (7:daily、12:monthly、52:weekly)
引用: http://alkaline-ml.com/pmdarima/tips_and_tricks.html
from pmdarima.arima import ndiffs
kpss_diffs = ndiffs(df.passengers_smoothed, alpha=0.05, test='kpss', max_d=10)
adf_diffs = ndiffs(df.passengers_smoothed, alpha=0.05, test='adf', max_d=10)
n_diffs = max(adf_diffs, kpss_diffs)
print(f"Estimated differencing term: {n_diffs}")Estimated differencing term: 0
d=0が良いようです。すでに定常過程のデータに変換しているので階差は0になると思っていましたが、予想通りでした。
(オプション) 季節orderのDの値をOCSB testで求める
# http://alkaline-ml.com/pmdarima/tips_and_tricks.html#period
from pmdarima.arima import nsdiffs
print(f"m=12: {nsdiffs(df.passengers_smoothed,m=12,max_D=7,test='ocsb')}")m=12: 0
m=12は月次の周期であることを表しています。テストの結果、D=0が良さそうです。
最適な次数のパラメータをpmdarimaで求め自動的にSARIMAモデルを作成する
「d」と「D」の値は事前に求めているのでそれぞれ0を指定します。
「m」はmonthlyを表す12にしました。
import numpy as np
import pmdarima as pm
# http://alkaline-ml.com/pmdarima/modules/generated/pmdarima.arima.AutoARIMA.html
stepwise_fit = pm.auto_arima(df.passengers_smoothed,
start_p=0, d=0, start_q=0,max_p=30, max_q=30,
seasonal=True, start_P=0, D=0, start_Q=0, max_P=10, max_Q=10, m=12,
max_order=100, trace=True, random_state=4649,
suppress_warnings=True, # warningsを出さないようにする
stepwise=True # stepwiseでやる
) Performing stepwise search to minimize aic ARIMA(0,0,0)(0,0,0)[12] intercept : AIC=-140.272, Time=0.09 sec ARIMA(1,0,0)(1,0,0)[12] intercept : AIC=inf, Time=0.51 sec ARIMA(0,0,1)(0,0,1)[12] intercept : AIC=-285.125, Time=0.26 sec ARIMA(0,0,0)(0,0,0)[12] : AIC=-122.662, Time=0.04 sec ARIMA(0,0,1)(0,0,0)[12] intercept : AIC=-224.953, Time=0.24 sec ARIMA(0,0,1)(1,0,1)[12] intercept : AIC=inf, Time=0.59 sec ARIMA(0,0,1)(0,0,2)[12] intercept : AIC=-317.435, Time=0.92 sec ARIMA(0,0,1)(1,0,2)[12] intercept : AIC=inf, Time=1.19 sec ARIMA(0,0,1)(0,0,3)[12] intercept : AIC=-332.542, Time=1.94 sec ARIMA(0,0,1)(1,0,3)[12] intercept : AIC=inf, Time=2.29 sec ARIMA(0,0,1)(0,0,4)[12] intercept : AIC=inf, Time=4.02 sec ARIMA(0,0,1)(1,0,4)[12] intercept : AIC=inf, Time=4.50 sec ARIMA(0,0,0)(0,0,3)[12] intercept : AIC=-284.061, Time=1.56 sec ARIMA(1,0,1)(0,0,3)[12] intercept : AIC=-355.221, Time=2.26 sec ARIMA(1,0,1)(0,0,2)[12] intercept : AIC=-333.068, Time=1.01 sec ARIMA(1,0,1)(1,0,3)[12] intercept : AIC=-424.942, Time=2.64 sec ARIMA(1,0,1)(1,0,2)[12] intercept : AIC=inf, Time=1.20 sec ARIMA(1,0,1)(2,0,3)[12] intercept : AIC=-419.123, Time=3.87 sec ARIMA(1,0,1)(1,0,4)[12] intercept : AIC=inf, Time=5.41 sec ARIMA(1,0,1)(0,0,4)[12] intercept : AIC=-363.888, Time=4.03 sec ARIMA(1,0,1)(2,0,2)[12] intercept : AIC=-420.241, Time=1.42 sec ARIMA(1,0,1)(2,0,4)[12] intercept : AIC=-423.595, Time=5.48 sec ARIMA(1,0,0)(1,0,3)[12] intercept : AIC=-427.218, Time=2.32 sec ARIMA(1,0,0)(0,0,3)[12] intercept : AIC=inf, Time=1.86 sec ARIMA(1,0,0)(1,0,2)[12] intercept : AIC=inf, Time=1.03 sec ARIMA(1,0,0)(2,0,3)[12] intercept : AIC=-422.947, Time=3.05 sec ARIMA(1,0,0)(1,0,4)[12] intercept : AIC=inf, Time=4.32 sec ARIMA(1,0,0)(0,0,2)[12] intercept : AIC=-332.443, Time=0.71 sec ARIMA(1,0,0)(0,0,4)[12] intercept : AIC=-365.619, Time=3.63 sec ARIMA(1,0,0)(2,0,2)[12] intercept : AIC=-426.668, Time=1.29 sec ARIMA(1,0,0)(2,0,4)[12] intercept : AIC=-423.391, Time=5.27 sec ARIMA(0,0,0)(1,0,3)[12] intercept : AIC=-366.233, Time=2.16 sec ARIMA(2,0,0)(1,0,3)[12] intercept : AIC=-426.257, Time=2.48 sec ARIMA(2,0,1)(1,0,3)[12] intercept : AIC=-422.609, Time=2.96 sec ARIMA(1,0,0)(1,0,3)[12] : AIC=-429.617, Time=1.86 sec ARIMA(1,0,0)(0,0,3)[12] : AIC=inf, Time=0.99 sec ARIMA(1,0,0)(1,0,2)[12] : AIC=inf, Time=0.74 sec ARIMA(1,0,0)(2,0,3)[12] : AIC=-424.909, Time=2.20 sec ARIMA(1,0,0)(1,0,4)[12] : AIC=inf, Time=4.32 sec ARIMA(1,0,0)(0,0,2)[12] : AIC=-331.898, Time=0.51 sec ARIMA(1,0,0)(0,0,4)[12] : AIC=-366.351, Time=3.66 sec ARIMA(1,0,0)(2,0,2)[12] : AIC=-429.532, Time=1.33 sec ARIMA(1,0,0)(2,0,4)[12] : AIC=-426.543, Time=4.64 sec ARIMA(0,0,0)(1,0,3)[12] : AIC=-366.377, Time=1.44 sec ARIMA(2,0,0)(1,0,3)[12] : AIC=-428.182, Time=2.12 sec ARIMA(1,0,1)(1,0,3)[12] : AIC=-427.643, Time=2.27 sec ARIMA(0,0,1)(1,0,3)[12] : AIC=-404.652, Time=2.66 sec ARIMA(2,0,1)(1,0,3)[12] : AIC=-425.529, Time=2.56 sec Best model: ARIMA(1,0,0)(1,0,3)[12] Total fit time: 107.877 seconds
SARIMA(1,0,0)(1,0,3)[12]が選択されました。
# ベストモデルのサマリ情報の確認
stepwise_fit.summary()
SARIMAX Results Dep. Variable: y No. Observations: 121 Model: SARIMAX(1, 0, 0)x(1, 0, [1, 2, 3], 12) Log Likelihood 220.809 Date: Tue, 01 Nov 2022 AIC -429.617 Time: 21:28:28 BIC -412.842 Sample: 12-01-1949 HQIC -422.804 - 12-01-1959 Covariance Type: opg
coef std err z P>|z| [0.025 0.975] ar.L1 0.6586 0.069 9.522 0.000 0.523 0.794 ar.S.L12 0.9893 0.011 91.639 0.000 0.968 1.010 ma.S.L12 -0.6074 0.115 -5.279 0.000 -0.833 -0.382 ma.S.L24 -0.0150 0.134 -0.112 0.911 -0.277 0.247 ma.S.L36 0.0397 0.134 0.296 0.767 -0.223 0.302 sigma2 0.0012 0.000 8.547 0.000 0.001 0.001
Ljung-Box (L1) (Q): 0.64 Jarque-Bera (JB): 4.97 Prob(Q): 0.42 Prob(JB): 0.08 Heteroskedasticity (H): 0.40 Skew: -0.16 Prob(H) (two-sided): 0.00 Kurtosis: 3.94
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
ma.S.L24とma.S.L36のP>|z|が0.05以上ですが、AICで見ているので気にしないことにします 笑
次は作成したモデルが適切かどうか残差分析をしてみます。
作成したSARIMAモデルの残差分析
残差の正規性はQQプロットで確認することにします。残差の間に相関がない(独立している)ことはLjung-Box検定で確認します。
resid = stepwise_fit.resid()
# SARIMA(1,0,0)(1,0,3)[12]の残差データを確認
resid.plot()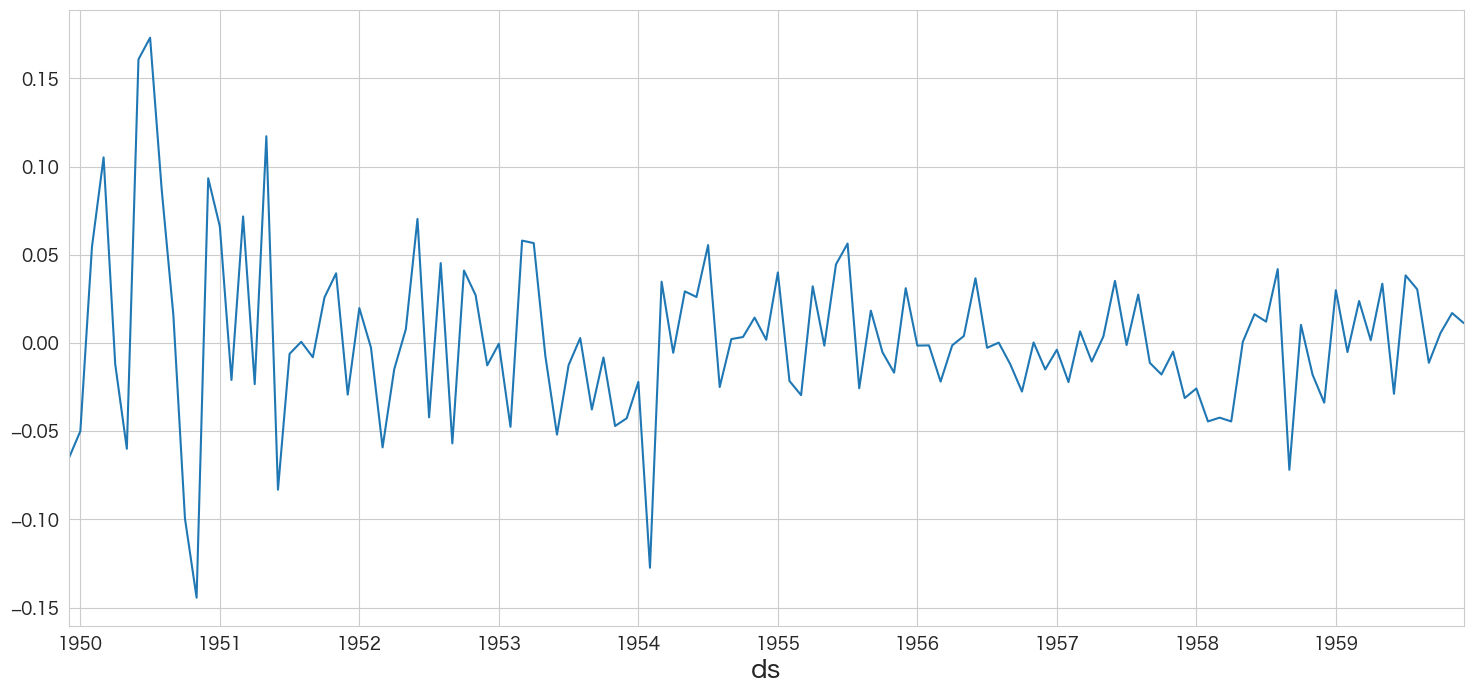
残差の平均と分散を確認
print(f"mean:{resid.mean()}、variance:{resid.var()}")mean:0.0022709552097981136、variance:0.0021746193193064997
残差の正規性の確認
# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt
plt.subplot(1,2,1)
sns.histplot(resid, kde=True)
plt.subplot(1,2,2)
stats.probplot(resid, dist="norm", plot=plt)
plt.show()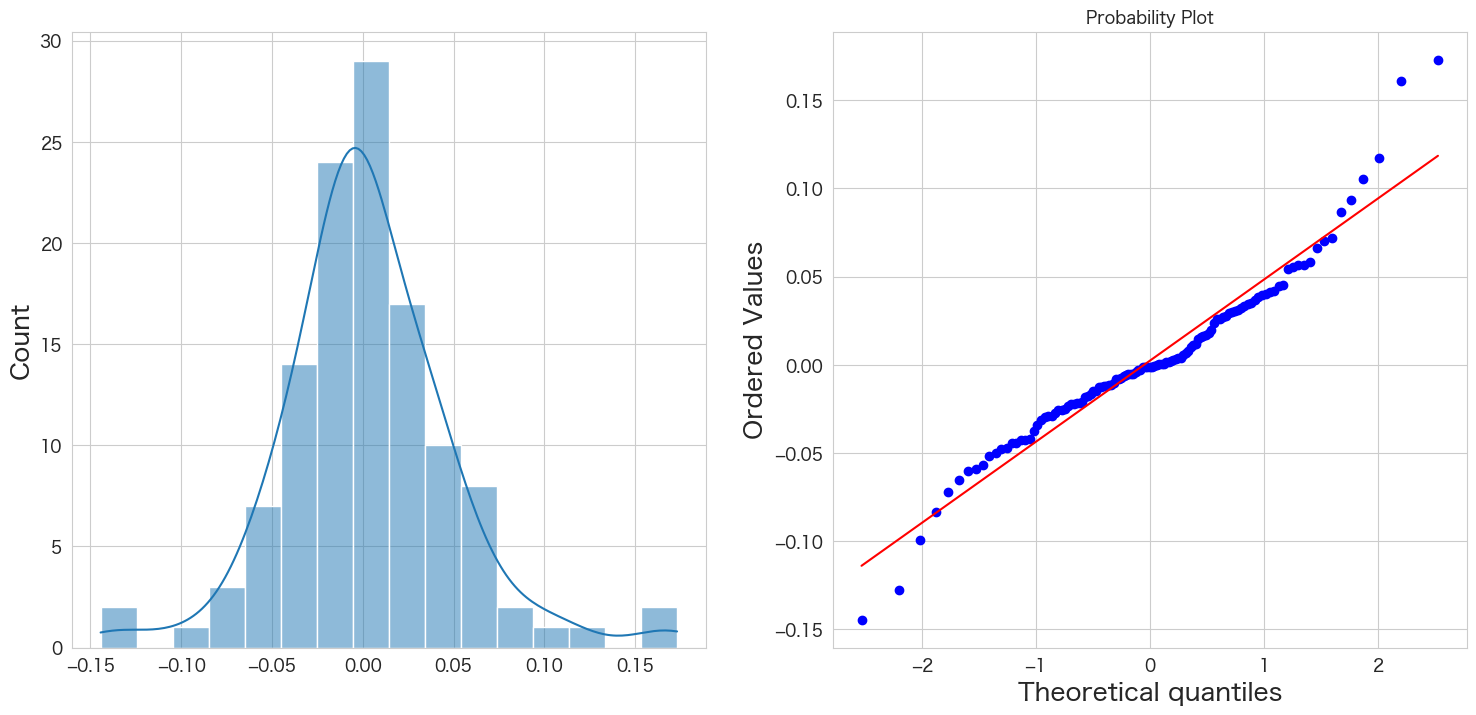
概ね正規分布に従っていそうです。
自己相関係数の確認
# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np
fig, ax = plt.subplots(figsize=(16,8))
plot_acf(resid, lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.show()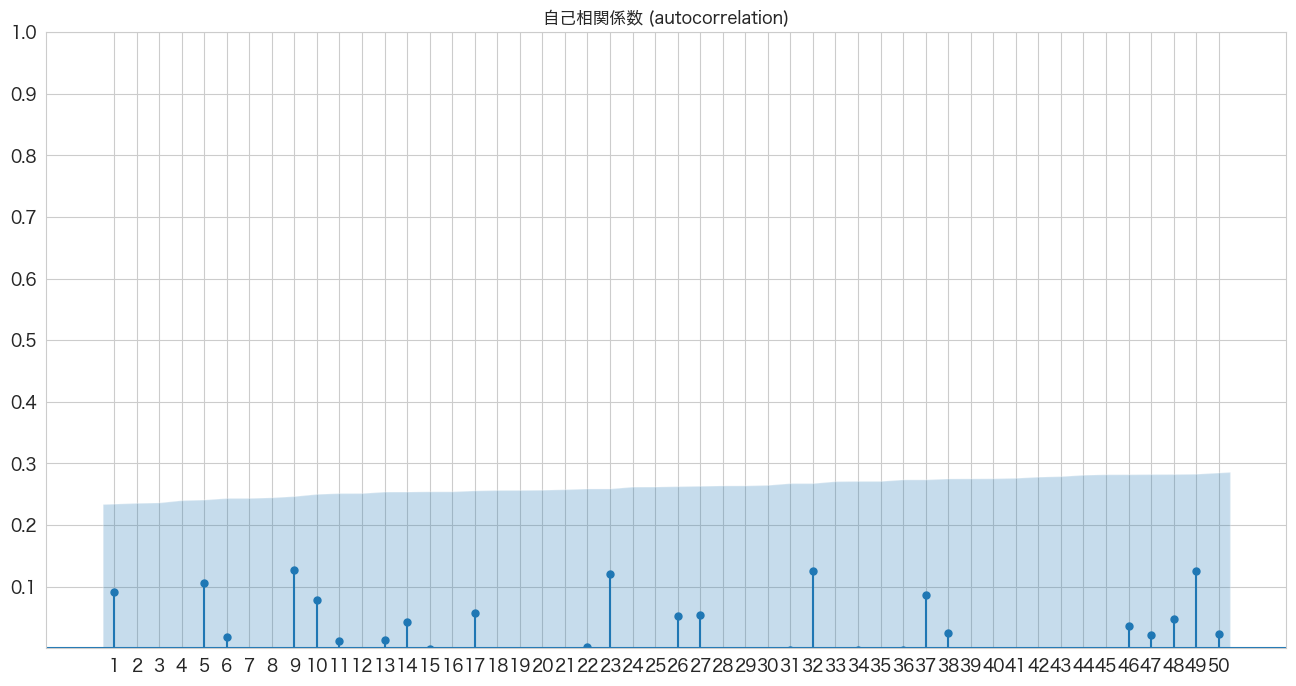
全て青いエリア内なので自己相関はなさそうですね。
Ljung-Box検定で残差の独立性の確認
仮説は下記になります。
H0: 残差は独立分布している
HA: 残差は独立分布ではない
残差が独立分布していることが望ましいので帰無仮説を棄却しない(P値 >= 0.05)結果になることを期待したいと思います。
# https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.acorr_ljungbox.html
import statsmodels.api as sm
sm.stats.acorr_ljungbox(resid)
# <div class="output_prompt">Out[0]</div>
# <pre class="outputcell nohighlight">| lb_stat | lb_pvalue | |
|---|---|---|
| 1 | 1.021318 | 0.312207 |
| 2 | 1.390700 | 0.498900 |
| 3 | 3.455763 | 0.326545 |
| 4 | 3.993803 | 0.406845 |
| 5 | 5.421127 | 0.366672 |
| 6 | 5.461095 | 0.486171 |
| 7 | 6.034967 | 0.535672 |
| 8 | 7.269618 | 0.507842 |
| 9 | 9.394441 | 0.401689 |
| 10 | 10.214481 | 0.421882 |
ARモデルとは違い、全て0.05以上なので帰無仮説は棄却されませんでした。良かったです。
残差分析の結果
残差分析の結果は、SARIMA(1,0,0)(1,0,3)[12]の残差が平均0の正規分布に従い、かつ残差の間には相関がないので問題なさそうです。
SARIMA(1,0,0)(1,0,3)[12]モデルを使って乗客数を予測する
作成したSARIMAモデルで乗客数を予測したいと思います。一体どうなるでしょうか?
1960-01 ~ 1960-12までの値を予測
# 1960-01 ~ 1960-12までの値を予測
stepwise_fit.predict(n_periods=12,X=df_test.index).plot()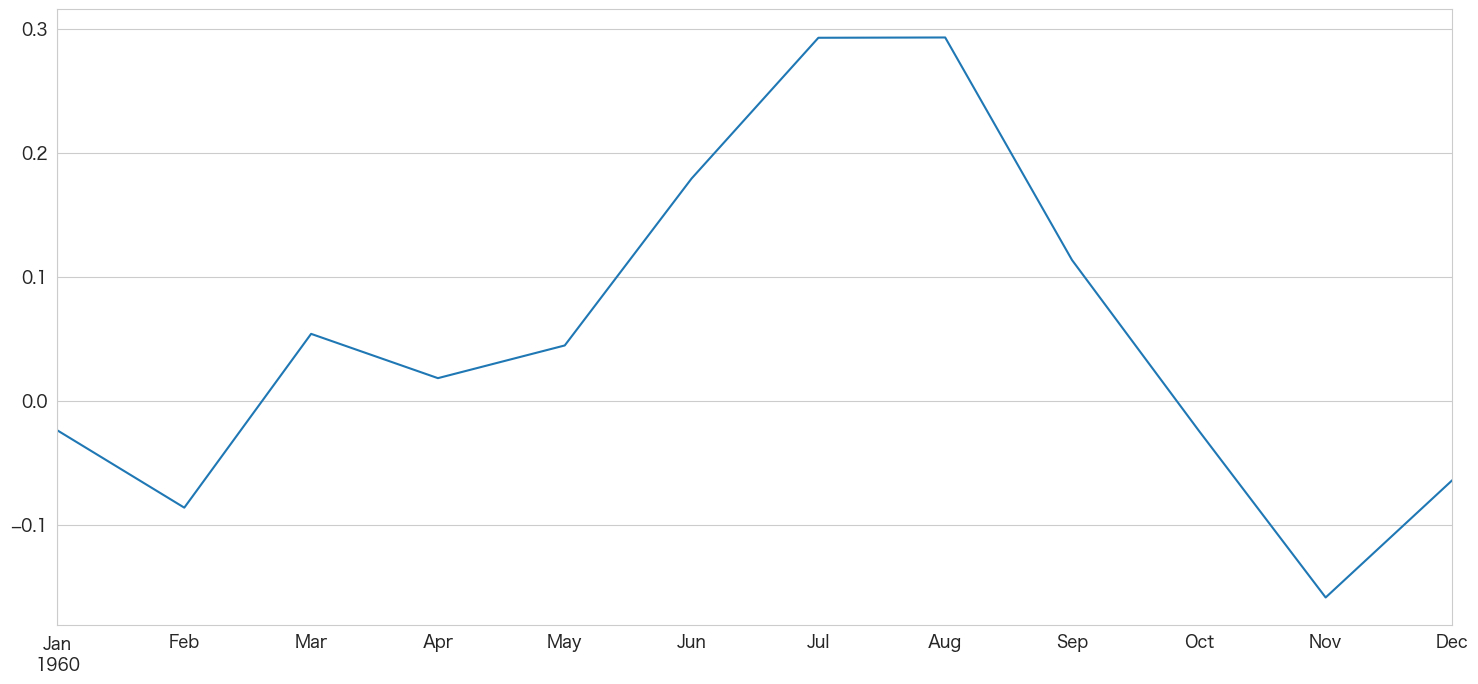
SARIMAモデルで求めた値は下記になるので、逆変換して「乗客数」を導き出します。
変換済み乗客数 = log(乗客数) - 12ヶ月の移動平均
移動平均値の予測モデルを作成
t時点の乗客数が分かっていないと移動平均値を出力できないので、単回帰で未来の移動平均値を予測してしまおうと思います。
詳細はARモデルの時にやっているので参照ください。
# 説明変数と目的変数を指定
X_train = df.index.values.astype(float).reshape(-1, 1) # 月次
Y_train = df["passengers_ma"] # 移動平均_乗客数
X_test = df_test.index.values.astype(float).reshape(-1, 1)
# 移動平均の予測のため学習
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(X_train,Y_train)変換済み乗客数と移動平均の予測
# 予測とデータ変換
df_test["pred_passengers_ma"] = model.predict(X_test)
df_test["pred_passengers_smoothed"] = stepwise_fit.predict(n_periods=12,X=df_test.index)
df_test["pred_passengers"] = np.power(np.e,(df_test.pred_passengers_smoothed + df_test.pred_passengers_ma))plt.figure(figsize=(20, 3))
# 訓練用とテスト用に分ける
ytrue = flights.passengers.iloc[:-12] # 訓練データの実数値
ypred = df_test.pred_passengers # 1960-01 ~ 1960-12の予測値
ytrue2 = flights.passengers.iloc[-12:] # 1960-01 ~ 1960-12の実測値
plt.plot(ytrue, label="Training Data")
plt.plot(ypred, label="Forecasts")
plt.plot(ytrue2, label="Test Data")
plt.title("airplane passengers prediction")
_ = plt.legend()
ARモデルよりは若干よくなったのかも知れませんが、見た目はそれほど劇的に変化があったようには見えませんでした。。MAEとかで精度を定量的に確認した方が分かりやすかったかも知れません。
まとめ
SARIMAモデルでも予測できました。
次はProphetを試してみようと思います。
本記事で利用したライブラリのバージョン
import pandas as pd
import numpy as np
import statsmodels as sm
import matplotlib as mpl
import pymannkendall as mk
import scipy as scp
print('pandas',pd.__version__)
print('numpy',np.__version__)
print('statsmodels',sm.__version__)
print('matplotlib',mpl.__version__)
print('pymannkendall',mk.__version__)
print('scipy',scp.__version__)pandas 1.4.3 numpy 1.23.2 statsmodels 0.13.2 matplotlib 3.5.3 pymannkendall 1.4.2 scipy 1.9.1