(その3-7) アップル引越しの需要予測をSARIMAモデルでやってみた

前回Auto-ARIMAモデルの記事を書きました。

(その3-6) アップル引越しの需要予測をAuto-ARIMAモデルでやってみた

前回ARMAモデルの記事を書きました。結果はARモデルやMAモデルと同じく1年分の日次予測は難しそうでした。今回は自動ARIMAモデルを試してみます。時系列モデル一覧 AR (自己回帰モデル) MA (移動平均モデル) ARMA (自...

結果はARMAモデルとそれほど変わりませんでしたが、自動的にARやMRの次数を効率的に求めてくれるので簡単にモデルを構築できました。

今回はSARIMAモデルを試してみます。

時系列モデル一覧

AR (自己回帰モデル)
MA (移動平均モデル)
ARMA (自己回帰移動平均モデル)
ARIMA (自己回帰和分移動平均モデル)
ARIMAX (自己回帰和分移動平均モデル with 外因性変数)
Auto ARIMA (自動ARIMAモデル)
SARIMA (季節ARIMAモデル)
SARIMAX (季節ARIMAモデル with 外因性変数)
ARCH (分散自己回帰モデル)
GARCH (一般化分散自己回帰モデル)
VAR (ベクトル自己回帰モデル)
VARMA (ベクトル自己回帰移動平均モデル)

SARIMAモデルはARIMAモデルに「S」easonal (季節/周期)の部分を考慮したモデルです。ARやMAの数値を増やすより一般的には良いとされているようです。

Sometimes a seasonal effect is suspected in the model; in that case, it is generally considered better to use a SARIMA (seasonal ARIMA) model than to increase the order of the AR or MA parts of the model.
引用: https://en.wikipedia.org/wiki/Autoregressive_integrated_moving_average

今回もARIMAモデルのときに利用したpmdarimaライブラリを利用しようと思います。SARIMAモデルも自動で作成出来るようになります。まだインストールしていなければ事前にpython3 -m pip install pmdarimaでライブラリをインストールしておきます。

アップル引越しの引越し数をSARIMAモデルで予想する
本記事で利用したライブラリのバージョン

アップル引越しの引越し数をSARIMAモデルで予想する

モデル作成するパートまではARモデルと共通になります。

本記事では重複した内容になってしまうので、詳細な説明を省きます。

データの読み込み

# アップル引越しのデータセットを読み込む
import pandas as pd
from matplotlib import pyplot as plt
import pandas as pd
# 訓練データと予測付与用データの読み込み
df = pd.read_csv("/Users/hinomaruc/Desktop/blog/dataset/applehikkoshi/train.csv",parse_dates=['datetime'],index_col='datetime')
df_test = pd.read_csv("/Users/hinomaruc/Desktop/blog/dataset/applehikkoshi/test.csv",parse_dates=['datetime'],index_col='datetime')

# 描画設定
from IPython.display import HTML
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12       # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12       # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18        # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8      # 画像サイズの変更(inch)

日付の間隔をasfreqメソッドで変更する

asfreqメソッドはpandasのメソッドで日付の粒度を変更してくれたり、足りない日付も作成してくれる便利なメソッドです。

# https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.asfreq.html
# 日付の間隔を「日間隔」に変更 (元から日別のデータですが、、週や月間隔にも変更できます)
df = df.asfreq('d')

df.info()

Out[0]

DatetimeIndex: 2101 entries, 2010-07-01 to 2016-03-31
Freq: D
Data columns (total 5 columns):
 #   Column    Non-Null Count  Dtype
---  ------    --------------  -----
 0   y         2101 non-null   int64
 1   client    2101 non-null   int64
 2   close     2101 non-null   int64
 3   price_am  2101 non-null   int64
 4   price_pm  2101 non-null   int64
dtypes: int64(5)
memory usage: 98.5 KB

欠損値の確認

df.infoメソッドで確認した通り、欠損値は今回存在しませんのでスキップします。

引っ越し数(y)を描画

pandasのplotメソッドで描画できます。

df.y.plot()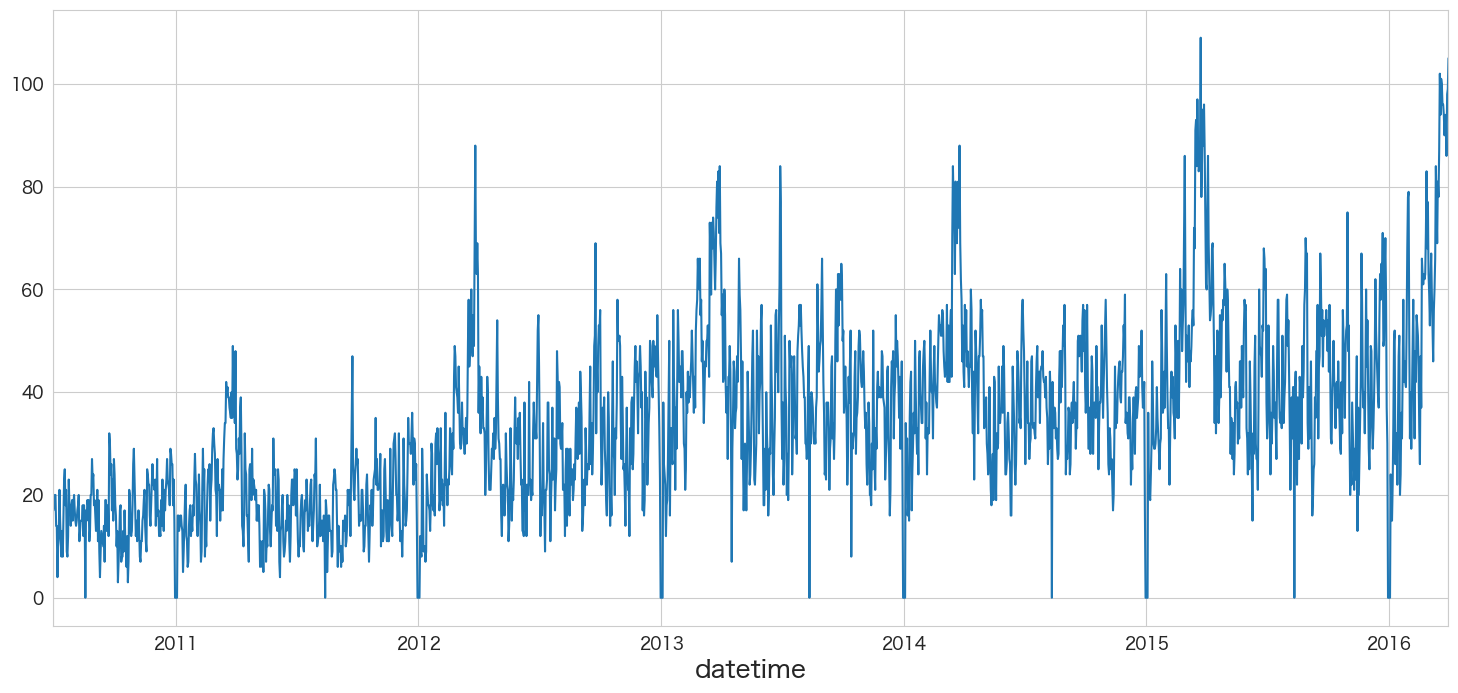

Out[0]

yが正規分布に従うかどうかQQプロットを確認

統計手法を適用するにあたり、おおよそ正規分布を仮定する必要があります。

そのためデータが正規分布に従っているかどうかQQプロットという手法を使って確認します。

# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt

plt.subplot(1,2,1)
sns.histplot(df["y"], kde=True)
plt.subplot(1,2,2)
stats.probplot(df["y"], dist="norm", plot=plt)
plt.show()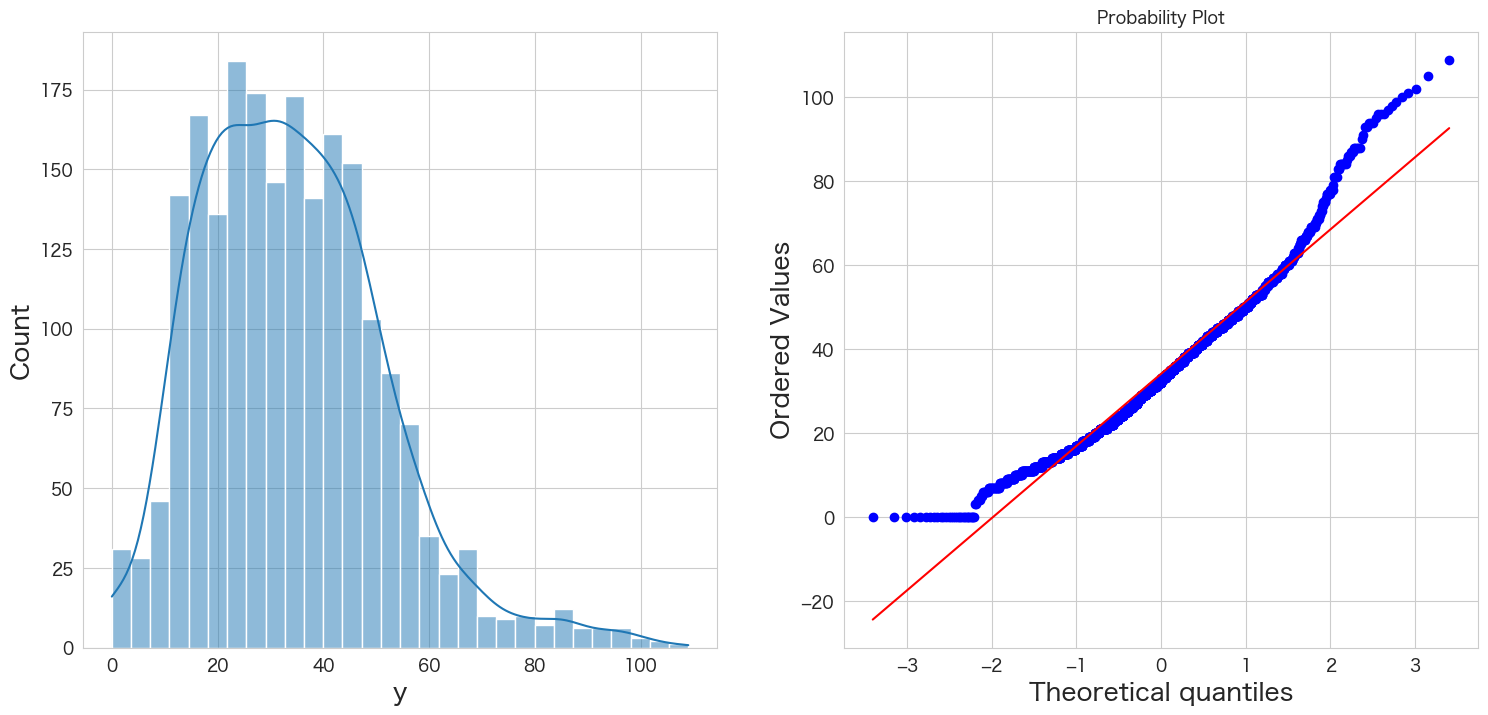

Out[0]

左側のグラフがヒストグラム、右側のグラフがQQプロットです。

青い点が赤い線に沿っていれば正規分布であるという表現方法になっています。

端の部分がずれているようですが、なんとなく正規分布に従っていると仮定します。

Mann-Kendall trend検定

H0: データにトレンドは存在しない
HA: データにトレンドが存在する

# https://pypi.org/project/pymannkendall/
import pymannkendall as mk
mk.original_test(df["y"])

Out[0]

Mann_Kendall_Test(trend='increasing', h=True, p=0.0, z=30.51302505819748, Tau=0.4440819564379774, s=979667.0, var_s=1030826418.3333334, slope=0.016624040920716114, intercept=14.544757033248079)

p <= 0.05なので帰無仮説は棄却され、データにトレンドは存在するという結果になりました。

そのため、拡張ディッキー・フラー検定ではトレンドがあるということを示すregression='ct'のオプションを追加しようと思います。

拡張ディッキー・フラー検定で時系列データが(弱)定常か非定常か確認する

帰無仮説と対立仮説は下記になります。

H0: 単位根がある
HA: 単位根がない

# https://www.statsmodels.org/dev/generated/statsmodels.tsa.stattools.adfuller.html
from statsmodels.tsa.stattools import adfuller

# 検定結果を見やすく加工
result = adfuller(df["y"],regression='ct')
labels = ["検定統計量","P値","#ラグ数","#観測数"]
mod_result = pd.Series(result[0:4],index=labels)
for key,val in result[4].items():
    mod_result[f'臨界値 (有意水準:{key})'] = val;
mod_result

Out[0]

検定統計量               -3.139726
P値                   0.097095
#ラグ数                26.000000
#観測数              2074.000000
臨界値 (有意水準:1%)       -3.963142
臨界値 (有意水準:5%)       -3.412609
臨界値 (有意水準:10%)      -3.128298
dtype: float64

P値が0.05以下ではないため帰無仮説を棄却できず「単位根がないとは言えない」という結果になります。

つまりアップル引っ越しのデータセットは弱定常過程ではなく、非定常過程の可能性がありそうです。

非定常過程のデータを定常過程のデータに変換する (階差)

SARIMAモデルも「I」ntegratedの部分で差分を取るので今回このパートはスキップします。

SARIMAモデルの作成

自動ARIMAモデルを実行する前に単純なSARIMA(1,1,1)(1,0,0,7)のモデル△y_t=c+ϕ₁△y_t-1 +θ₁ε_t-1+ε_t+S(𝜙₇y_t−7 + 𝜙₈y_t−8)を作成していこうと思います。

式の中身を分解すると下記になります。

・cはコンスタント値
・△y_tは現在の値と1ピリオド前の値の差分
・△y_t-1は1ピリオド前の値の2ピリオド前の値の差分
・ε_tは現在の残差(エラー)
・ε_t-1は1ピリオド前の残差(エラー)
・ϕは現在値を説明するのに過去の値がどれほど関連しているか (ARの部分)
・θは現在値を説明するのに過去の残差(エラー)がどれほど関連しているか (MAの部分)
・Sは季節コンポーネントの部分(1季節を7ピリオドとした場合の値)

Sも含めるとどんどん複雑なモデルになっていきますね、それではSARIMAモデルの作成をしていきたいと思います。

from statsmodels.tsa.arima.model import ARIMA
# SARIMA(1,1,1)(1,0,0,7)モデルの作成
sarima_model111_1007 = ARIMA(df.y,order=(1,1,1),seasonal_order=(1,0,0,7))
sarima_model111_1007_fit = sarima_model111_1007.fit()
sarima_model111_1007_fit.summary()

Out[0]



SARIMAX Results

  Dep. Variable:                  y                 No. Observations:     2101   


  Model:            ARIMA(1, 1, 1)x(1, 0, [], 7)    Log Likelihood      -7475.956


  Date:                   Fri, 23 Sep 2022          AIC                 14959.913


  Time:                       15:06:14              BIC                 14982.512


  Sample:                    07-01-2010             HQIC                14968.190


                           - 03-31-2016                                         


  Covariance Type:               opg                                             




             coef      std err       z       P>|z|   [0.025     0.975]  


  ar.L1        0.6689      0.017     40.300   0.000      0.636      0.701


  ma.L1       -0.9587      0.007   -130.286   0.000     -0.973     -0.944


  ar.S.L7      0.2466      0.021     12.017   0.000      0.206      0.287


  sigma2      72.3524      1.672     43.268   0.000     69.075     75.630




  Ljung-Box (L1) (Q):      9.91    Jarque-Bera (JB):   253.12


  Prob(Q):                 0.00    Prob(JB):            0.00 


  Heteroskedasticity (H):  2.48    Skew:                -0.12


  Prob(H) (two-sided):     0.00    Kurtosis:            4.68 



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

SARIMAX Results
Dep. Variable:	y	No. Observations:	2101
Model:	ARIMA(1, 1, 1)x(1, 0, [], 7)	Log Likelihood	-7475.956
Date:	Fri, 23 Sep 2022	AIC	14959.913
Time:	15:06:14	BIC	14982.512
Sample:	07-01-2010	HQIC	14968.190
	- 03-31-2016
Covariance Type:	opg

	coef	std err	z	P>\|z\|	[0.025	0.975]
ar.L1	0.6689	0.017	40.300	0.000	0.636	0.701
ma.L1	-0.9587	0.007	-130.286	0.000	-0.973	-0.944
ar.S.L7	0.2466	0.021	12.017	0.000	0.206	0.287
sigma2	72.3524	1.672	43.268	0.000	69.075	75.630

Ljung-Box (L1) (Q):	9.91	Jarque-Bera (JB):	253.12
Prob(Q):	0.00	Prob(JB):	0.00
Heteroskedasticity (H):	2.48	Skew:	-0.12
Prob(H) (two-sided):	0.00	Kurtosis:	4.68

ar.S.L7という係数が出てきました、これが季節の部分だと思われます。

(オプション) 階差の最適な数値を求める

SARIMAモデルの「I」の部分の値を求めます。

auto-SARIMAで自動的に求めてくれるようですが、明示的に値をオプションに指定してあげることによって処理が効率化されるようです。

下記にサンプルがあるので、そのまま利用します。

Stock market prediction — pmdarima 2.0.3 documentation

from pmdarima.arima import ndiffs

kpss_diffs = ndiffs(df.y, alpha=0.05, test='kpss', max_d=10)
adf_diffs = ndiffs(df.y, alpha=0.05, test='adf', max_d=10)
n_diffs = max(adf_diffs, kpss_diffs)

print(f"Estimated differencing term: {n_diffs}")

Out[0]

Estimated differencing term: 1

SARIMAの「I」は1が良さそうという結果になりました。

(オプション) 季節orderのDの値をOCSB testで求める

こちらも先に求めておくことで処理が早くなるようなので必要であればやっておきます。

# http://alkaline-ml.com/pmdarima/tips_and_tricks.html#period
from pmdarima.arima import nsdiffs
print(f"m=7: {nsdiffs(df.y,m=7,max_D=7,test='ocsb')}")
print(f"m=12: {nsdiffs(df.y,m=12,max_D=7,test='ocsb')}")
print(f"m=30: {nsdiffs(df.y,m=30,max_D=7,test='ocsb')}")
print(f"m=52: {nsdiffs(df.y,m=52,max_D=7,test='ocsb')}")
print(f"m=365: {nsdiffs(df.y,m=365,max_D=7,test='ocsb')}")

Out[0]

m=7: 0
m=12: 0
m=30: 0
m=52: 0
m=365: 0

今回はどのmでもD=0を設定すると良いようです。

pmdarimaで自動SARIMAモデルを作成する

SARIMAモデルもpmdarimaライブラリを使えば、自動的に次数を探索してくれます。
dとDの値は事前に1.10と1.11で求めておいた値を利用します。(d=1,D=0)

import numpy as np
import pmdarima as pm

# http://alkaline-ml.com/pmdarima/modules/generated/pmdarima.arima.AutoARIMA.html
stepwise_fit = pm.auto_arima(df.y, 
                                            start_p=0, d=1, start_q=0,max_p=50, max_q=50,
                                            seasonal=True, start_P=0, D=0, start_Q=0, max_P=5, max_Q=5, m=7,
                                            max_order=100, trace=True, random_state=4649,
                                            suppress_warnings=True,  # warningsを出さないようにする
                                            stepwise=True # stepwiseでやる
                                             )

Out[0]


Performing stepwise search to minimize aic
 ARIMA(0,1,0)(0,0,0)[7] intercept   : AIC=15355.426, Time=0.09 sec
 ARIMA(1,1,0)(1,0,0)[7] intercept   : AIC=15119.850, Time=0.87 sec
 ARIMA(0,1,1)(0,0,1)[7] intercept   : AIC=15129.432, Time=0.73 sec
 ARIMA(0,1,0)(0,0,0)[7]             : AIC=15353.468, Time=0.05 sec
 ARIMA(1,1,0)(0,0,0)[7] intercept   : AIC=15280.829, Time=0.11 sec
 ARIMA(1,1,0)(2,0,0)[7] intercept   : AIC=15063.260, Time=1.68 sec
 ARIMA(1,1,0)(3,0,0)[7] intercept   : AIC=15017.387, Time=4.43 sec
 ARIMA(1,1,0)(4,0,0)[7] intercept   : AIC=14986.826, Time=7.93 sec
 ARIMA(1,1,0)(5,0,0)[7] intercept   : AIC=14962.050, Time=13.12 sec
 ARIMA(1,1,0)(5,0,1)[7] intercept   : AIC=inf, Time=35.22 sec
 ARIMA(1,1,0)(4,0,1)[7] intercept   : AIC=inf, Time=20.84 sec
 ARIMA(0,1,0)(5,0,0)[7] intercept   : AIC=15149.516, Time=8.12 sec
 ARIMA(2,1,0)(5,0,0)[7] intercept   : AIC=14929.375, Time=15.98 sec
 ARIMA(2,1,0)(4,0,0)[7] intercept   : AIC=14953.460, Time=9.72 sec
 ARIMA(2,1,0)(5,0,1)[7] intercept   : AIC=inf, Time=37.77 sec
 ARIMA(2,1,0)(4,0,1)[7] intercept   : AIC=inf, Time=25.84 sec
 ARIMA(3,1,0)(5,0,0)[7] intercept   : AIC=14925.829, Time=16.22 sec
 ARIMA(3,1,0)(4,0,0)[7] intercept   : AIC=14950.593, Time=9.61 sec
 ARIMA(3,1,0)(5,0,1)[7] intercept   : AIC=inf, Time=46.41 sec
 ARIMA(3,1,0)(4,0,1)[7] intercept   : AIC=inf, Time=25.46 sec
 ARIMA(4,1,0)(5,0,0)[7] intercept   : AIC=14912.694, Time=18.79 sec
 ARIMA(4,1,0)(4,0,0)[7] intercept   : AIC=14932.830, Time=12.45 sec
 ARIMA(4,1,0)(5,0,1)[7] intercept   : AIC=inf, Time=47.72 sec
 ARIMA(4,1,0)(4,0,1)[7] intercept   : AIC=inf, Time=32.86 sec
 ARIMA(5,1,0)(5,0,0)[7] intercept   : AIC=14876.126, Time=24.16 sec
 ARIMA(5,1,0)(4,0,0)[7] intercept   : AIC=14895.843, Time=13.40 sec
 ARIMA(5,1,0)(5,0,1)[7] intercept   : AIC=inf, Time=59.63 sec
 ARIMA(5,1,0)(4,0,1)[7] intercept   : AIC=inf, Time=34.88 sec
 ARIMA(6,1,0)(5,0,0)[7] intercept   : AIC=14877.112, Time=27.76 sec
 ARIMA(5,1,1)(5,0,0)[7] intercept   : AIC=14877.450, Time=26.86 sec
 ARIMA(4,1,1)(5,0,0)[7] intercept   : AIC=inf, Time=50.41 sec
 ARIMA(6,1,1)(5,0,0)[7] intercept   : AIC=14878.556, Time=66.86 sec
 ARIMA(5,1,0)(5,0,0)[7]             : AIC=14874.199, Time=5.84 sec
 ARIMA(5,1,0)(4,0,0)[7]             : AIC=14893.923, Time=3.75 sec
 ARIMA(5,1,0)(5,0,1)[7]             : AIC=inf, Time=38.72 sec
 ARIMA(5,1,0)(4,0,1)[7]             : AIC=inf, Time=25.16 sec
 ARIMA(4,1,0)(5,0,0)[7]             : AIC=14910.741, Time=4.96 sec
 ARIMA(6,1,0)(5,0,0)[7]             : AIC=14875.191, Time=7.61 sec
 ARIMA(5,1,1)(5,0,0)[7]             : AIC=14875.527, Time=8.53 sec
 ARIMA(4,1,1)(5,0,0)[7]             : AIC=inf, Time=20.13 sec
 ARIMA(6,1,1)(5,0,0)[7]             : AIC=14876.640, Time=14.12 sec

Best model:  ARIMA(5,1,0)(5,0,0)[7]          
Total fit time: 824.866 seconds

SARIMA(5,1,0)(5,0,0)[7]が選択されました。

m=7でいいのかは要検討です。MAコンポーネントはなしでARだけになりました。これではSARIモデルですね　笑

# ベストモデルのサマリ情報の確認
stepwise_fit.summary()

Out[0]



SARIMAX Results

  Dep. Variable:                  y                  No. Observations:     2101   


  Model:            SARIMAX(5, 1, 0)x(5, 0, 0, 7)    Log Likelihood      -7426.100


  Date:                   Fri, 23 Sep 2022           AIC                 14874.199


  Time:                       21:48:41               BIC                 14936.346


  Sample:                    07-01-2010              HQIC                14896.962


                           - 03-31-2016                                          


  Covariance Type:               opg                                              




              coef      std err       z       P>|z|   [0.025     0.975]  


  ar.L1        -0.3574      0.017    -20.536   0.000     -0.392     -0.323


  ar.L2        -0.1821      0.021     -8.580   0.000     -0.224     -0.140


  ar.L3        -0.1221      0.021     -5.817   0.000     -0.163     -0.081


  ar.L4        -0.1488      0.020     -7.368   0.000     -0.188     -0.109


  ar.L5        -0.1421      0.020     -7.210   0.000     -0.181     -0.103


  ar.S.L7       0.1205      0.020      5.887   0.000      0.080      0.161


  ar.S.L14      0.0686      0.021      3.277   0.001      0.028      0.110


  ar.S.L21      0.1019      0.021      4.903   0.000      0.061      0.143


  ar.S.L28      0.1312      0.021      6.254   0.000      0.090      0.172


  ar.S.L35      0.1031      0.021      4.836   0.000      0.061      0.145


  sigma2       68.9652      1.632     42.247   0.000     65.766     72.165




  Ljung-Box (L1) (Q):      0.02    Jarque-Bera (JB):   257.79


  Prob(Q):                 0.89    Prob(JB):            0.00 


  Heteroskedasticity (H):  2.39    Skew:                -0.27


  Prob(H) (two-sided):     0.00    Kurtosis:            4.63 



Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).

SARIMAX Results
Dep. Variable:	y	No. Observations:	2101
Model:	SARIMAX(5, 1, 0)x(5, 0, 0, 7)	Log Likelihood	-7426.100
Date:	Fri, 23 Sep 2022	AIC	14874.199
Time:	21:48:41	BIC	14936.346
Sample:	07-01-2010	HQIC	14896.962
	- 03-31-2016
Covariance Type:	opg

	coef	std err	z	P>\|z\|	[0.025	0.975]
ar.L1	-0.3574	0.017	-20.536	0.000	-0.392	-0.323
ar.L2	-0.1821	0.021	-8.580	0.000	-0.224	-0.140
ar.L3	-0.1221	0.021	-5.817	0.000	-0.163	-0.081
ar.L4	-0.1488	0.020	-7.368	0.000	-0.188	-0.109
ar.L5	-0.1421	0.020	-7.210	0.000	-0.181	-0.103
ar.S.L7	0.1205	0.020	5.887	0.000	0.080	0.161
ar.S.L14	0.0686	0.021	3.277	0.001	0.028	0.110
ar.S.L21	0.1019	0.021	4.903	0.000	0.061	0.143
ar.S.L28	0.1312	0.021	6.254	0.000	0.090	0.172
ar.S.L35	0.1031	0.021	4.836	0.000	0.061	0.145
sigma2	68.9652	1.632	42.247	0.000	65.766	72.165

Ljung-Box (L1) (Q):	0.02	Jarque-Bera (JB):	257.79
Prob(Q):	0.89	Prob(JB):	0.00
Heteroskedasticity (H):	2.39	Skew:	-0.27
Prob(H) (two-sided):	0.00	Kurtosis:	4.63

P>|z|は全てが0.05以下なので意味がある係数ということになり問題なさそうです。

作成したSARIMAモデルの残差分析

残差の正規性はQQプロットで確認することにします。残差の間に相関がない(独立している)ことはLjung-Box検定で確認します。

resid = stepwise_fit.resid()
# SARIMA(5,1,0)(5,0,0)[7]の残差データを確認
resid.plot()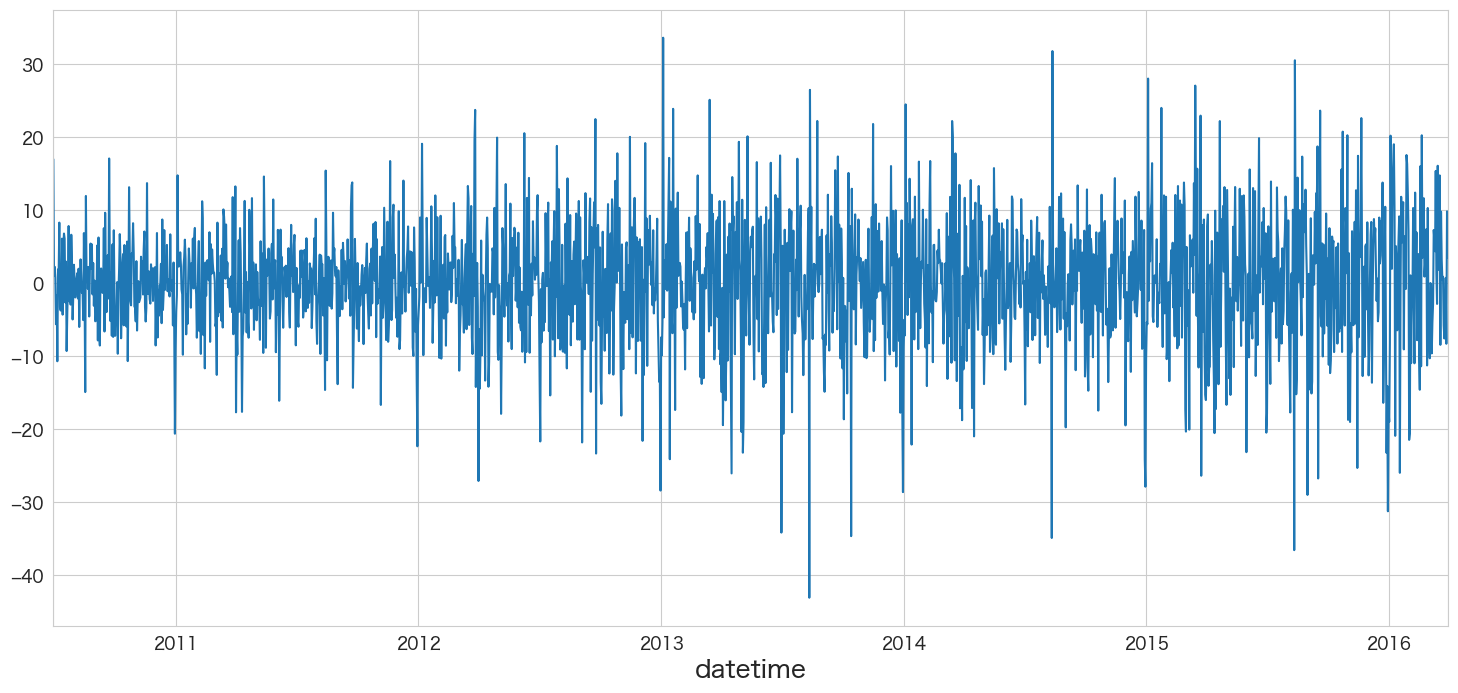

Out[0]

残差の平均と分散を確認

print(f"mean:{resid.mean()}、variance:{resid.var()}")

Out[0]

mean:0.05973608491309389、variance:69.11913207331469

残差の正規性の確認

# 正規分布に従うかどうかをQQプロットを描画して確認
import scipy.stats as stats
import matplotlib.pyplot as plt

plt.subplot(1,2,1)
sns.histplot(resid, kde=True)
plt.subplot(1,2,2)
stats.probplot(resid, dist="norm", plot=plt)
plt.show()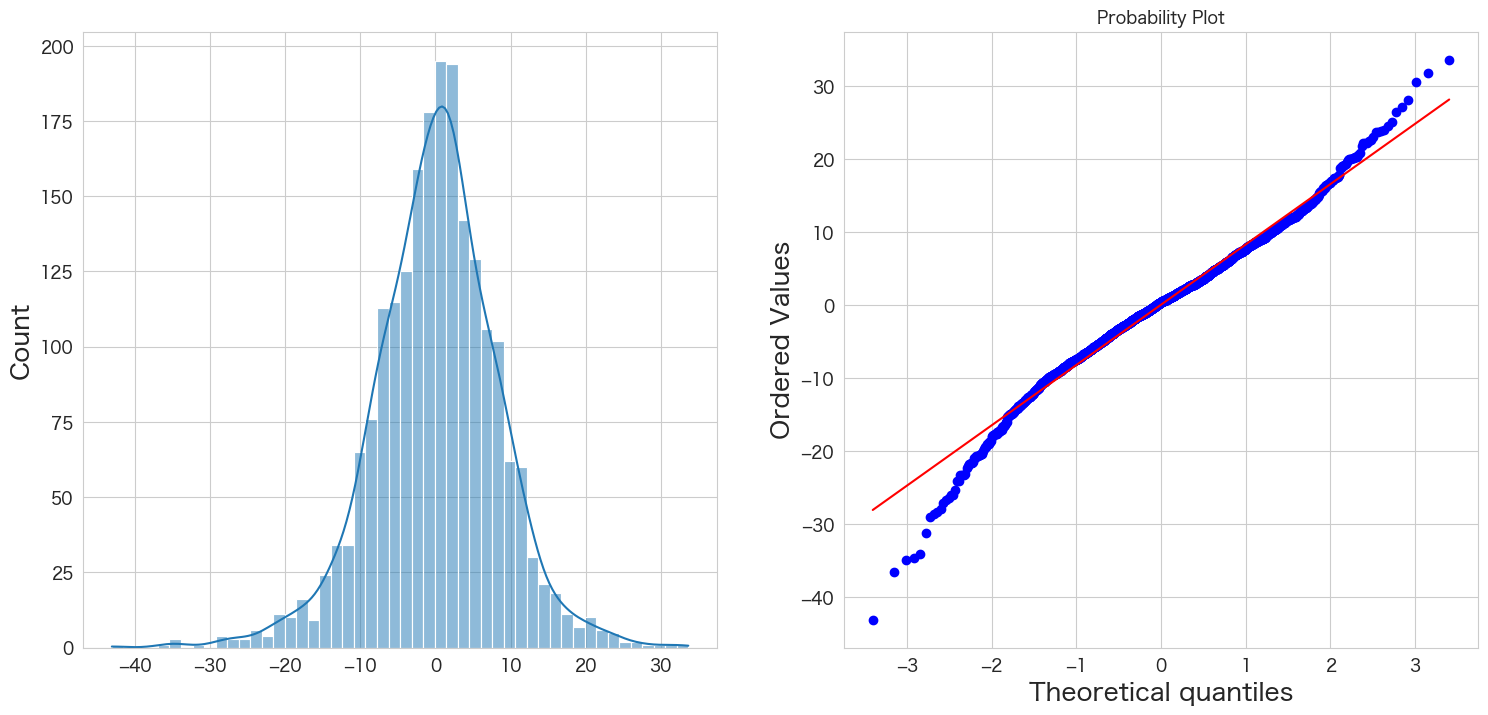

Out[0]

概ね正規分布に従っていそうです。

自己相関係数の確認

# 自己相関係数の確認
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
import numpy as np

fig, ax = plt.subplots(figsize=(16,8))
plot_acf(resid, lags=50, zero=False, title="自己相関係数 (autocorrelation)", ax=ax, alpha=0.01)
plt.ylim([0,1])
plt.yticks(np.arange(0.1, 1.1, 0.1))
plt.xticks(np.arange(1, 51, 1))
plt.show()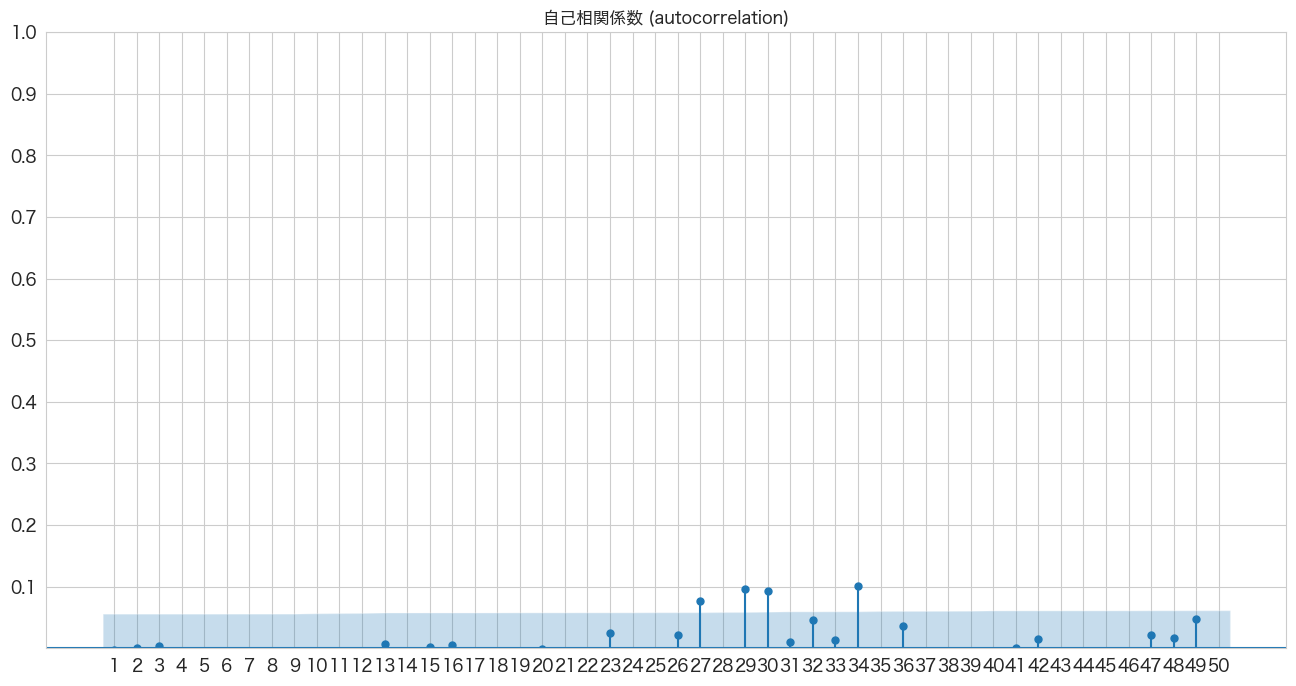

Out[0]

若干青いエリアから外れていますが概ね問題なさそうです。

Ljung-Box検定で残差の独立性の確認

H0: 残差は独立分布している
HA: 残差は独立分布ではない

残差が独立分布していることが望ましいので帰無仮説を棄却しない(P値 >= 0.05)結果になることを期待したいと思います。

# https://www.statsmodels.org/stable/generated/statsmodels.stats.diagnostic.acorr_ljungbox.html

import statsmodels.api as sm
sm.stats.acorr_ljungbox(resid,lags=10)

Out[0]

	lb_stat	lb_pvalue
1	0.016195	0.898734
2	0.017392	0.991342
3	0.056409	0.996496
4	0.177986	0.996267
5	0.773249	0.978708
6	2.222825	0.898107
7	2.293631	0.941820
8	3.994863	0.857587
9	25.725832	0.002265
10	38.153032	0.000036

1~10のラグで検定してみました。ラグ9とラグ10以外の全てのp値が0.05以上なので問題ないということにします。

残差分析の結果

残差分析の結果は、SARIMA(5,1,0)(5,0,0)[7]の残差が平均0の正規分布に従い、一応ラグ8まで残差の間には相関がないので問題ないということにします。

SARIMA(5,1,0)(5,0,0)[7]モデルを使って引っ越し数を予測する

季節性が含まれることによってどう変化するのでしょうか

# 2016-04-01 ~ 2017-03-31までの階差を予測
stepwise_fit.predict(n_periods=365,X=df_test.index).plot()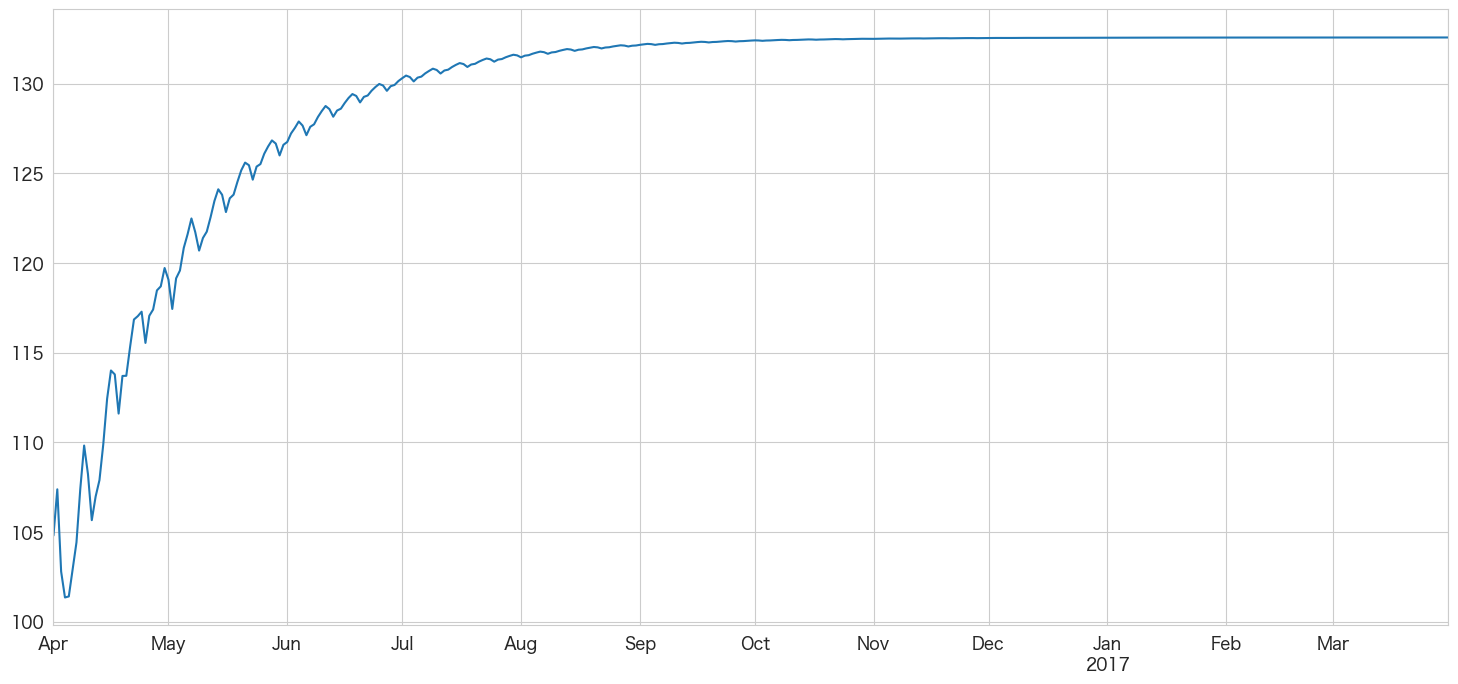

Out[0]

# 学習データの引っ越し数の値(青い線)と予測した引っ越し数の値(オレンジの線)を描画
plt.figure(figsize=(20, 3))

ytrue = df.y.iloc[-31:]
ypred = stepwise_fit.predict(n_periods=365,X=df_test.index)

plt.plot(ytrue, label="Training Data")
plt.plot(ypred, label="Forecasts")

plt.title("apple-hikkoshi prediction")
_ = plt.legend()

Out[0]

SARIMAモデルでも日次データで1年後を予測するのは難しいのでしょうか？まずは月次で予測して追加情報として使うみたいにやった方がいいのかも知れません。

(番外編) 季節/周期(m)の数値を変更して幾つか結果を見てみる

from statsmodels.tsa.arima.model import ARIMA
# SARIMA(35,1,28)(5,0,1,30)モデルの作成
sarima_model = ARIMA(df.y,order=(35,1,28),seasonal_order=(5,0,1,30))
sarima_model_fit = sarima_model.fit()
sarima_model_fit.summary()

下記エラーが発生しました。non-季節コンポーネントと季節コンポーネントで重複するラグがあると起きるようです。

ValueError: Invalid model: autoregressive lag(s) {30} are in both the seasonal and non-seasonal autoregressive components.

低次数の簡単なモデルにして再挑戦

from statsmodels.tsa.arima.model import ARIMA
# SARIMA(1,1,1)(2,0,1,12)モデルの作成 m=12,30,52,365を試した。
sarima_model = ARIMA(df.y,order=(1,1,1),seasonal_order=(2,0,1,12))
sarima_model_fit = sarima_model.fit()

# 学習データの引っ越し数の値(青い線)と予測した引っ越し数の値(オレンジの線)を描画
plt.figure(figsize=(20, 3))

ytrue = df.y.iloc[-31:]
ypred = sarima_model_fit.predict(start = df_test.index[0],end = df_test.index[-1])

plt.plot(ytrue, label="Training Data")
plt.plot(ypred, label="Forecasts")

plt.title("apple-hikkoshi prediction")
_ = plt.legend()

Out[0]

m=12

m=30

m=52

m=365
20分待っても処理が終わらず断念

mの値が増えるにつれて結果も徐々に変化があることがわかる。

まとめ

SARIMAモデルでも1年分の日別予測は難しかったです。状態空間モデルやXgboostなども試そうと思いましたが、一旦ここまでにしておきます。今のところ時系列モデルを作成するときはProphetが一番よかったですね。

(その3-2) アップル引越しの需要予測をProphetでやってみた

今回はMeta社のProphetというツールを使ってみたいと思います。 Prophet is a forecasting procedure implemented in R and Python. It is fast and provi...

本記事で利用したライブラリのバージョン

import pandas as pd
import numpy as np
import statsmodels as sm
import matplotlib as mpl
import pymannkendall as mk
import scipy as scp
print('pandas',pd.__version__)
print('numpy',np.__version__)
print('statsmodels',sm.__version__)
print('matplotlib',mpl.__version__)
print('pymannkendall',mk.__version__)
print('scipy',scp.__version__)

Out[0]

pandas 1.4.3
numpy 1.23.2
statsmodels 0.13.2
matplotlib 3.5.3
pymannkendall 1.4.2
scipy 1.9.1