前回の記事ではタイタニックのデータセットの特徴量エンジニアリングの作業をしました。
今回は 4 変数選択 (Feature Selection)の作業をしようと思います。
こちらの記事で変数選択では相関係数とVIFの値算出をしようと考えていました。
相関係数とVIFの値を算出し、多重共線性の確認をしたいと思います。
その上でどちらかの変数を採用するなど決めたいと思います。
よく相関係数の確認はしていたのですが、VIFはやったことがありませんでした。
どういう結果になるのか楽しみです。
多重共線性(multicollinearity)が存在することの影響
過去の記事で変数選択の1つとして「相関が高い一方の変数を除外をすることによって、多重共線性を防ぎ安定したモデルを作成する」と書きました。おまじないように言っていましたが、後学のためもう少し突っ込んで調べてみました。
なぜ多重共線性が存在するとモデルが不安定になるのかというと、偏回帰係数の分散の幅が大きくなるためのようです。
単変数の少しの変化でも大幅に反応したり係数の符号逆転現象(プラスマイナスが逆になる)が発生したりという結果1になりやすいようですが、係数が不安定で信頼できる解釈が難しくなるというだけで、相関が高い変数がそれぞれの結果を打ち消しあうため「予測の良さ」には影響しないようです。2
また回帰問題だけでなく、多重共線性の問題は分類問題でも起きるようです。具体的には変数の重要度を計算し確認したときに信頼できない値や順番になることがあるようです。*3
・偏回帰係数の分散についてはこちらの記事のシュミレーションが直感的で分かりやすかったです。
・多重共線性の解決方法についてはこちらの記事が例題も記載されていて分かりやすかったです。
変数選択のための事前作業
相関係数やVIFを計算するために今まで実施した欠損値処理や特徴量エンジニアリングの作業を先にやります。
タイタニックのデータセットの読み込み
import pandas as pd
import numpy as np
# タイタニックデータセットの訓練データを読み込み
df = pd.read_csv("/Users/hinomaruc/Desktop/notebooks/titanic/train.csv")# 描画設定
import seaborn as sns
from matplotlib import ticker
import matplotlib.pyplot as plt
sns.set_style("whitegrid")
from matplotlib import rcParams
rcParams['font.family'] = 'Hiragino Sans' # Macの場合
#rcParams['font.family'] = 'Meiryo' # Windowsの場合
#rcParams['font.family'] = 'VL PGothic' # Linuxの場合
rcParams['xtick.labelsize'] = 12 # x軸のラベルのフォントサイズ
rcParams['ytick.labelsize'] = 12 # y軸のラベルのフォントサイズ
rcParams['axes.labelsize'] = 18 # ラベルのフォントとサイズ
rcParams['figure.figsize'] = 18,8 # 画像サイズの変更(inch)Embarkedの欠損値処理
# fill missing value for Embarked column
from sklearn.impute import SimpleImputer
# missing_values = int, float, str, np.nan or None
imp = SimpleImputer(missing_values=np.nan, strategy="most_frequent")
imp.fit(np.array(df.loc[:,"Embarked"]).reshape(-1,1))
df["Embarked"] = imp.transform(np.array(df.loc[:,"Embarked"]).reshape(-1,1))特徴量エンジニアリング
# the number of family member travelling with. including him/her self
df['FamilyCnt'] = df['SibSp'] + df['Parch'] + 1
# The number of members who may travel with using the same ticket number. probably correlated to FamilyCnt
df["SameTicketCnt"] = df.groupby('Ticket')["Ticket"].transform('count')from sklearn.preprocessing import OneHotEncoder
enc = OneHotEncoder(categories='auto',handle_unknown='ignore') #エラーは0になるオプション
# change datatype of Pclass to str for creating dummpy variables
df['Pclass_str'] = df['Pclass'].apply(str)
# fit to create dummy variables
enc.fit(df[['Pclass_str','Sex','Embarked']])OneHotEncoder(handle_unknown='ignore')
# OneHotEncoderでダミー化した変数をDataFrameに追加
cols=enc.get_feature_names_out(['Pclass_str','Sex','Embarked'])
df = df.join(pd.DataFrame(enc.transform(df[['Pclass_str','Sex','Embarked']]).toarray(),columns=cols))# Pclass_strはもう使わないので削除する
df = df.drop(columns=["Pclass_str"])Ageの欠損値処理
XgBoostで欠損値のAgeを推定します。
XgBoostのための訓練データ作成
df_train = df.dropna(subset=['Age'])XgBoostのためのテストデータ作成
# データ読み込み
df_test = pd.read_csv("/Users/hinomaruc/Desktop/notebooks/titanic/test.csv")
# Pclassをstr型に変更
df_test['Pclass_str'] = df_test['Pclass'].apply(str)
# ダミー変数の作成
df_test = df_test.join(pd.DataFrame(enc.transform(df_test[['Pclass_str','Sex','Embarked']]).toarray(),columns=cols))
# drop unnessesary column(s)
df_test = df_test.drop(columns=["Pclass_str"])
# AgeとFareが欠損しているレコードを除外
df_test = df_test.dropna(subset=['Age', 'Fare'])
# the number of family member travelling with. including him/her self
df_test['FamilyCnt'] = df_test['SibSp'] + df_test['Parch'] + 1
# The number of members who may travel with using the same ticket number. probably correlated to FamilyCnt
df_test["SameTicketCnt"] = df_test.groupby('Ticket')["Ticket"].transform('count')xgboostでAgeの推定
# 投入変数
# FamilyCntとSameTicketCntを含めると結果が微妙だったので学習からは外しています。
FEATURE_COLS=[
# 'PassengerId'
# , 'Survived'
# , 'Pclass'
# , 'Name'
# , 'Sex'
# 'Age'
'SibSp'
, 'Parch'
# , 'Ticket'
, 'Fare'
# , 'Cabin'
# , 'Embarked'
# , 'FamilyCnt'
# , 'SameTicketCnt'
, 'Pclass_str_1'
, 'Pclass_str_2'
, 'Pclass_str_3'
, 'Sex_female'
, 'Sex_male'
, 'Embarked_C'
, 'Embarked_Q'
, 'Embarked_S'
]
X_train = df_train[FEATURE_COLS] # 説明変数 (train)
Y_train = df_train["Age"] # 目的変数 (train)
X_test = df_test[FEATURE_COLS] # 説明変数 (test)
Y_test = df_test["Age"] # 目的変数 (test)# 自由度調整済みr2を算出
def adjusted_r2(X,Y,model):
from sklearn.metrics import r2_score
import numpy as np
r_squared = r2_score(Y, model.predict(X))
adjusted_r2 = 1 - (1-r_squared)*(len(Y)-1)/(len(Y)-X.shape[1]-1)
return adjusted_r2# モデル評価指標算出
def get_model_evaluations(X_train,Y_train,X_test,Y_test,model):
from sklearn.metrics import explained_variance_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_squared_log_error
from sklearn.metrics import median_absolute_error
# 評価指標確認
# 参考: https://funatsu-lab.github.io/open-course-ware/basic-theory/accuracy-index/
yhat_test = model.predict(X_test)
return "adjusted_r2(train) :" + str(adjusted_r2(X_train,Y_train,model)) \
, "adjusted_r2(test) :" + str(adjusted_r2(X_test,Y_test,model)) \
, "平均誤差率(test) :" + str(np.mean(abs((yhat_test - Y_test) / yhat_test))) \
, "MAE(test) :" + str(mean_absolute_error(Y_test, yhat_test)) \
, "MedianAE(test) :" + str(median_absolute_error(Y_test, yhat_test)) \
, "RMSE(test) :" + str(np.sqrt(mean_squared_error(Y_test, yhat_test))) \
, "RMSE(test) / MAE(test) :" + str(np.sqrt(mean_squared_error(Y_test, yhat_test)) / mean_absolute_error(Y_test, yhat_test)) #better if result = 1.253import xgboost as xgb
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import KFold
# Grid Search用のパラメータ作成。
# あまり組み合わせが多いと時間がかかる
params = {
'eta': [0.1,0.2,0.3], # default = 0.3
'gamma': [3,4,5], # default = 0
'max_depth': [1,2,3], # default = 6
'min_child_weight': [0,1,2], # default = 1
'subsample': [0.7,0.8,0.9], # default = 1
'colsample_bytree': [0,0.1,0.2], # default = 1
}
# K-分割交差検証
kf = KFold(n_splits = 5, shuffle = True, random_state = 1)
# モデル定義
model = xgb.XGBRegressor(objective ='reg:squarederror')
# Gridサーチ定義
grid = GridSearchCV(estimator=model, param_grid=params, scoring='neg_mean_squared_error', n_jobs=2, cv=kf.split(X_train,Y_train), verbose=3)# fitで学習させる
grid.fit(X_train,Y_train)
Fitting 5 folds for each of 729 candidates, totalling 3645 fits
[CV 1/5] END colsample_bytree=0.2, eta=0.3, gamma=3, max_depth=3, min_child_weight=2, subsample=0.8;, score=-150.826 total time= 0.1s
[CV 1/5] END colsample_bytree=0.2, eta=0.3, gamma=3, max_depth=3, min_child_weight=2, subsample=0.9;, score=-150.716 total time= 0.1s
[CV 2/5] END colsample_bytree=0.2, eta=0.3, gamma=3, max_depth=3, min_child_weight=2, subsample=0.9;, score=-166.139 total time= 0.1s
・・・省略・・・
[CV 4/5] END colsample_bytree=0.2, eta=0.3, gamma=3, max_depth=3, min_child_weight=2, subsample=0.7;, score=-180.948 total time= 0.1s
[CV 2/5] END colsample_bytree=0.2, eta=0.3, gamma=3, max_depth=3, min_child_weight=2, subsample=0.8;, score=-166.136 total time= 0.1s
[CV 3/5] END colsample_bytree=0.2, eta=0.3, gamma=3, max_depth=3, min_child_weight=2, subsample=0.8;, score=-166.545 total time= 0.1s
GridSearchCV(cv=,
estimator=XGBRegressor(base_score=None, booster=None,
colsample_bylevel=None,
colsample_bynode=None,
colsample_bytree=None,
enable_categorical=False, gamma=None,
gpu_id=None, importance_type=None,
interaction_constraints=None,
learning_rate=None, max_delta_step=None,
max_depth=None, min_child_weight...
num_parallel_tree=None, predictor=None,
random_state=None, reg_alpha=None,
reg_lambda=None, scale_pos_weight=None,
subsample=None, tree_method=None,
validate_parameters=None, verbosity=None),
n_jobs=2,
param_grid={'colsample_bytree': [0, 0.1, 0.2],
'eta': [0.1, 0.2, 0.3], 'gamma': [3, 4, 5],
'max_depth': [1, 2, 3], 'min_child_weight': [0, 1, 2],
'subsample': [0.7, 0.8, 0.9]},
scoring='neg_mean_squared_error', verbose=3)
# 学習結果確認
print('ベストスコア:',grid.best_score_, sep="\n")
print('\n')
print('ベストestimator:',grid.best_estimator_,sep="\n")
print('\n')
print('ベストparams:',grid.best_params_,sep="\n")
ベストスコア:
-154.8612261342364
ベストestimator:
XGBRegressor(base_score=0.5, booster='gbtree', colsample_bylevel=1,
colsample_bynode=1, colsample_bytree=0.2, enable_categorical=False,
eta=0.1, gamma=4, gpu_id=-1, importance_type=None,
interaction_constraints='', learning_rate=0.100000001,
max_delta_step=0, max_depth=3, min_child_weight=2, missing=nan,
monotone_constraints='()', n_estimators=100, n_jobs=1,
num_parallel_tree=1, predictor='auto', random_state=0, reg_alpha=0,
reg_lambda=1, scale_pos_weight=1, subsample=0.7,
tree_method='exact', validate_parameters=1, verbosity=None)
ベストparams:
{'colsample_bytree': 0.2, 'eta': 0.1, 'gamma': 4, 'max_depth': 3, 'min_child_weight': 2, 'subsample': 0.7}
# Grid Searchで一番精度が良かったモデル
bestmodel = grid.best_estimator_# 精度確認
get_model_evaluations(X_train,Y_train,X_test,Y_test,bestmodel)
('adjusted_r2(train) :0.34846460953290725',
'adjusted_r2(test) :0.25853312032424125',
'平均誤差率(test) :0.3329817762116459',
'MAE(test) :9.376575835881997',
'MedianAE(test) :7.426568984985352',
'RMSE(test) :11.923044182744015',
'RMSE(test) / MAE(test) :1.2715776410741828')
plt.figure()
ax = sns.regplot(x=Y_test, y=bestmodel.predict(X_test), fit_reg=False,color='#4F81BD')
ax.set_xlabel(u"Age")
ax.set_ylabel(u"(Predicted) Age")
ax.get_xaxis().set_major_formatter(ticker.FuncFormatter(lambda x, p: format(int(x), ',')))
ax.get_yaxis().set_major_formatter(ticker.FuncFormatter(lambda y, p: format(int(y), ',')))
ax.plot([0,10,20,30,40,50],[0,10,20,30,40,50], linewidth=2, color="#C0504D",ls="--")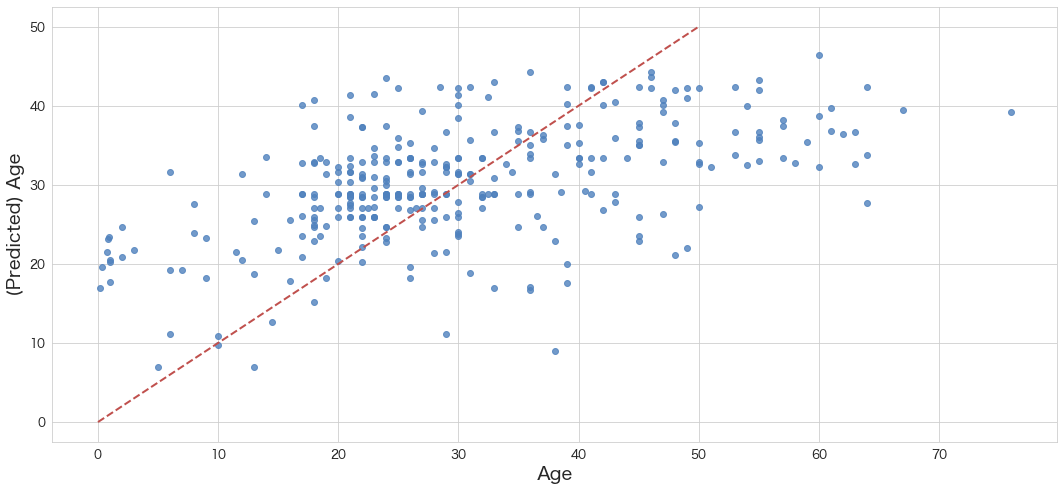
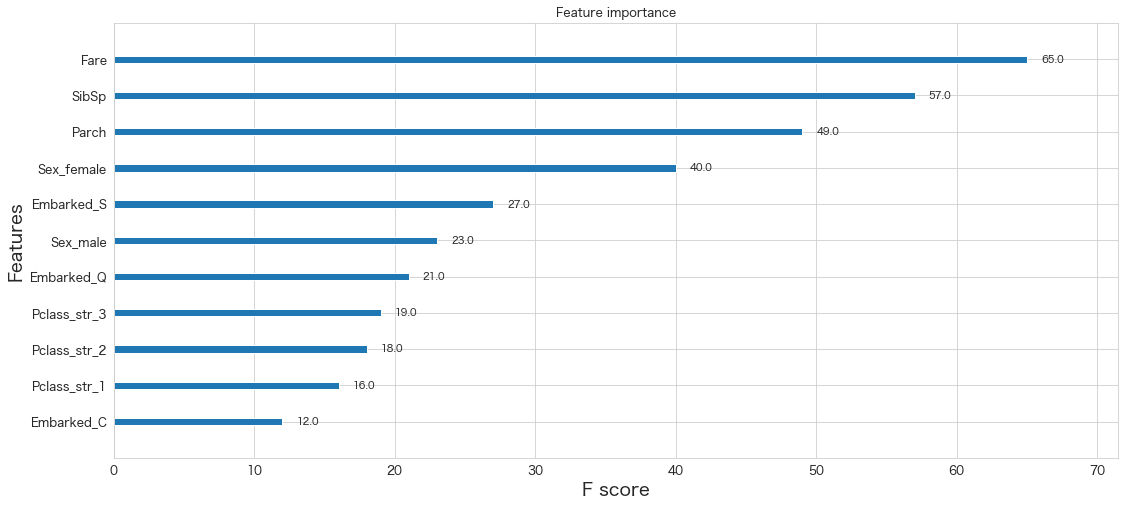
xgb.plot_importance(bestmodel)<AxesSubplot:title={'center':'Feature importance'}, xlabel='F score', ylabel='Features'>
# save xgboost model
bestmodel.save_model("age_prediction.json")df["Age_predicted"] = bestmodel.predict(df[FEATURE_COLS])df[["Age","Age_predicted"]]
Age Age_predicted 0 22.0 27.118692 1 38.0 36.228737 2 26.0 25.893398 3 35.0 37.435017 4 35.0 28.812716 ... ... ... 886 27.0 33.368904 887 19.0 37.941185 888 NaN 15.693979 889 26.0 42.368938 890 32.0 31.638159 891 rows × 2 columns
# Ageの欠損値をAge_predictedで補完してあげる
df.Age = np.where(df.Age.isnull(), df.Age_predicted, df.Age)# 置換結果確認
df[["Age","Age_predicted"]]
Age Age_predicted 0 22.000000 27.118692 1 38.000000 36.228737 2 26.000000 25.893398 3 35.000000 37.435017 4 35.000000 28.812716 ... ... ... 886 27.000000 33.368904 887 19.000000 37.941185 888 15.693979 15.693979 889 26.000000 42.368938 890 32.000000 31.638159 891 rows × 2 columns
無事置換されているようです。
# 使用しないカラムを削除
df = df.drop(columns=["Age_predicted"])変数選択
変数選択の準備までが長かったですが、相関係数とVIFを確認して多重共線性の疑いがある変数は削除しようと思います。
予測するだけであれば多重共線性は気にしなくてもよさそうですが、モデル解釈が難しくなったり変数重要度が判断できなくなるようなので私はきちんとやりたいと思います。
ダミー変数として作成したPclass_str_2、Sex_male、Embarked_Cは事前に除外しています。(例えばSexからSex_maleとSex_femaleというダミー変数を作成したらどちらか一方の変数を除外した)
これはダミー変数トラップと呼ばれるダミー変数を作成したときに起きる完全多重共線性を防ぐためです。
VIFを計算するときにinfという結果になってしまう方はダミー変数がそのまま投入されていないか確認をしてみてください。
私がテストした限り、1組のダミー変数だと問題ありませんでしたが、2組以上完全多重共線性を持つダミー変数を投入してしまうとVIFの結果がinfになりました。
ダミー変数トラップに関しての詳細はOne-Hot-Encoding, Multicollinearity and the Dummy Variable Trapの記事がサンプルも載っていてわかりやすかったです。
相関係数の確認 ①
FEATURE_COLS=[
# 'PassengerId'
'Survived'
# , 'Pclass'
# , 'Name'
# , 'Sex'
, 'Age'
, 'SibSp'
, 'Parch'
# , 'Ticket'
, 'Fare'
# , 'Cabin'
# , 'Embarked'
, 'FamilyCnt'
, 'SameTicketCnt'
, 'Pclass_str_1'
#, 'Pclass_str_2'
, 'Pclass_str_3'
, 'Sex_female'
# , 'Sex_male'
# , 'Embarked_C'
, 'Embarked_Q'
, 'Embarked_S'
]
df_train = df[FEATURE_COLS] # 学習用データ# 相関係数の確認
sns.heatmap(round(df_train.corr(),1), vmax=1, vmin=-1, center=0,annot=True)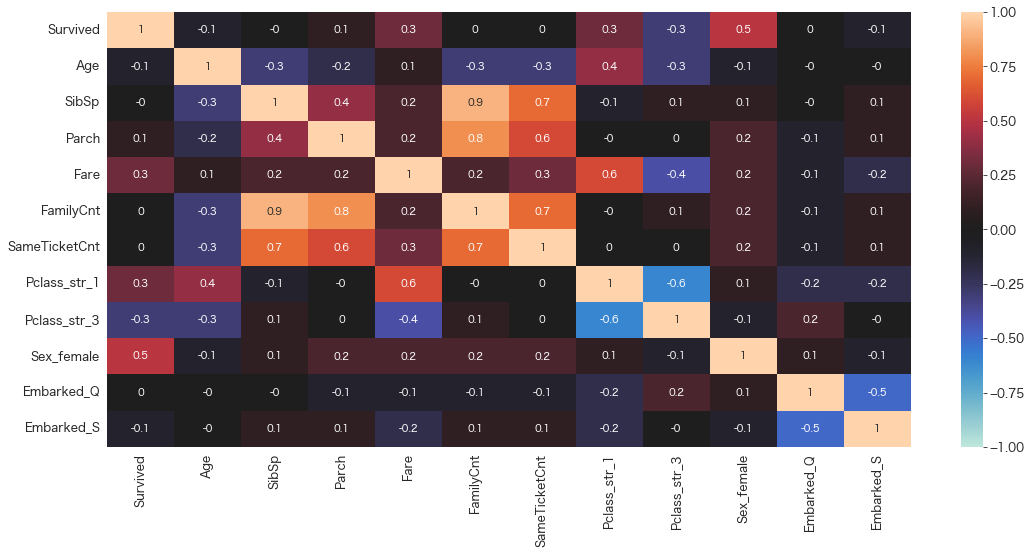
見た感じ、FamilyCnt x SibSp、FamilyCnt x SameTicketCntあたりは相関係数が0.7以上あるのでどちらか一方を除外した方がいいかもしれません。
全体像を掴んだ上で、さっそくVIFで確認してみます。
VIFの確認 ①
# 参考: https://www.geeksforgeeks.org/detecting-multicollinearity-with-vif-python/
from statsmodels.stats.outliers_influence import variance_inflation_factor
# VIF dataframe
vif_data = pd.DataFrame()
# 変数名を格納
vif_data["feature"] = df_train.columns
vif_data
feature 0 Survived 1 Age 2 SibSp 3 Parch 4 Fare 5 FamilyCnt 6 SameTicketCnt 7 Pclass_str_1 8 Pclass_str_3 9 Sex_female 10 Embarked_Q 11 Embarked_S
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(df_train.values, i) for i in range(len(df_train.columns))]
vif_data
feature VIF 0 Survived 1.669636 1 Age 1.444274 2 SibSp 36.901178 3 Parch 19.767075 4 Fare 1.932195 5 FamilyCnt 145.401924 6 SameTicketCnt 2.526117 7 Pclass_str_1 2.426784 8 Pclass_str_3 1.883290 9 Sex_female 1.539005 10 Embarked_Q 1.498383 11 Embarked_S 1.518021
VIFが5以上は多重共線性の疑いがありますので、SibSp,Parch,FamilyCntのうち1つの変数に絞った方が良さそうです。
今回はせっかく作成したので、FamilyCntを選びます。
FamilyCntを選択し、さらにVIFの計算と確認を繰り返します。
相関係数の確認 ②
FEATURE_COLS=[
# 'PassengerId'
'Survived'
# , 'Pclass'
# , 'Name'
# , 'Sex'
, 'Age'
# , 'SibSp'
#, 'Parch'
# , 'Ticket'
, 'Fare'
# , 'Cabin'
# , 'Embarked'
, 'FamilyCnt'
, 'SameTicketCnt'
, 'Pclass_str_1'
#, 'Pclass_str_2'
, 'Pclass_str_3'
, 'Sex_female'
# , 'Sex_male'
# , 'Embarked_C'
, 'Embarked_Q'
, 'Embarked_S'
]
df_train = df[FEATURE_COLS] # 学習用データ# 相関係数の確認
sns.heatmap(round(df_train.corr(),1), vmax=1, vmin=-1, center=0,annot=True)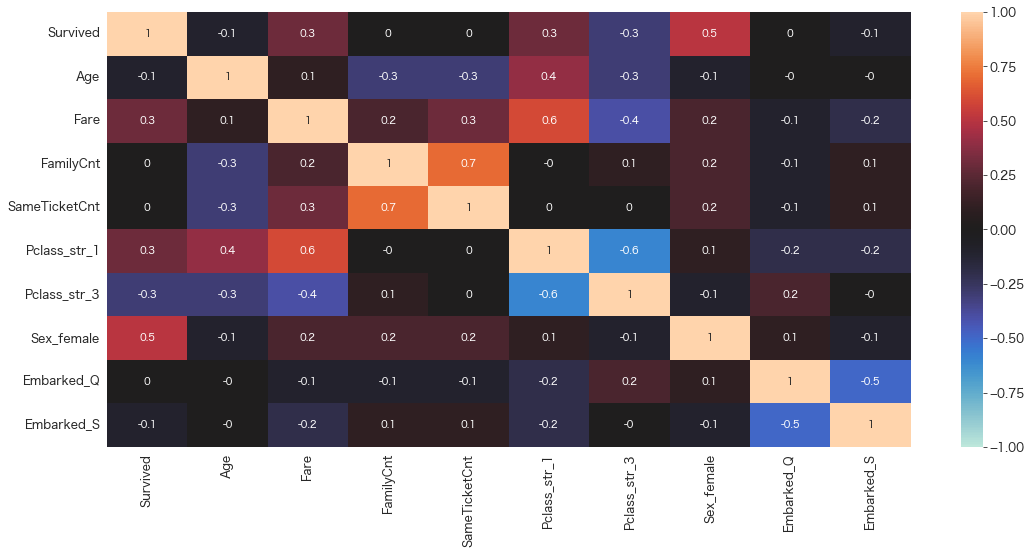
VIFの確認 ②
from statsmodels.stats.outliers_influence import variance_inflation_factor
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = df_train.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(df_train.values, i) for i in range(len(df_train.columns))]
vif_data
feature VIF 0 Survived 2.446505 1 Age 4.869462 2 Fare 2.717797 3 FamilyCnt 5.700519 4 SameTicketCnt 6.791496 5 Pclass_str_1 3.107809 6 Pclass_str_3 2.920084 7 Sex_female 2.345591 8 Embarked_Q 1.550484 9 Embarked_S 4.304881
FamilyCntとSameTicketCntも関係しあっていそうです。同行者としてまとまっていそうなSameTicketCntを選択します。
さらに繰り返します。
相関係数の確認 ③
FEATURE_COLS=[
# 'PassengerId'
'Survived'
# , 'Pclass'
# , 'Name'
# , 'Sex'
, 'Age'
# , 'SibSp'
#, 'Parch'
# , 'Ticket'
, 'Fare'
# , 'Cabin'
# , 'Embarked'
# , 'FamilyCnt'
, 'SameTicketCnt'
, 'Pclass_str_1'
#, 'Pclass_str_2'
, 'Pclass_str_3'
, 'Sex_female'
# , 'Sex_male'
# , 'Embarked_C'
, 'Embarked_Q'
, 'Embarked_S'
]
df_train = df[FEATURE_COLS] # 学習用データ# 相関係数の確認
sns.heatmap(round(df_train.corr(),1), vmax=1, vmin=-1, center=0,annot=True)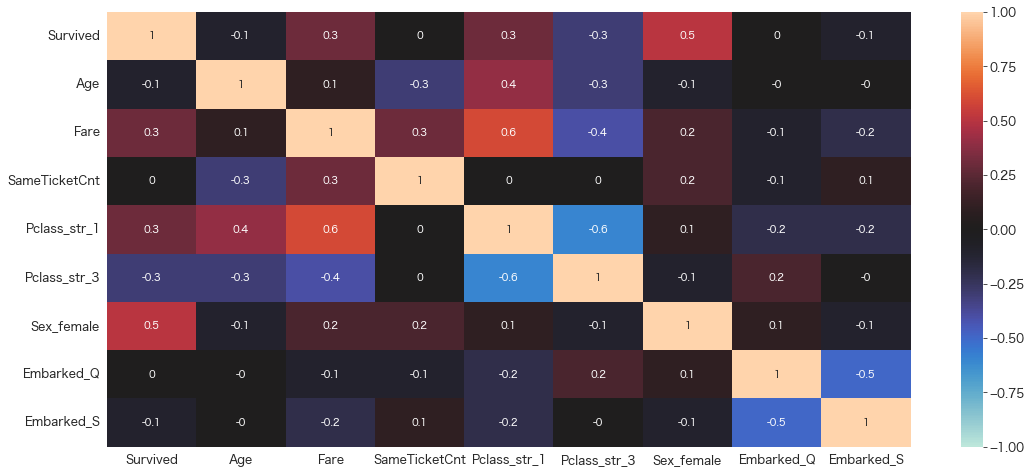
VIFの確認 ③
from statsmodels.stats.outliers_influence import variance_inflation_factor
# VIF dataframe
vif_data = pd.DataFrame()
vif_data["feature"] = df_train.columns
# calculating VIF for each feature
vif_data["VIF"] = [variance_inflation_factor(df_train.values, i) for i in range(len(df_train.columns))]
vif_data
feature VIF 0 Survived 2.439416 1 Age 4.827689 2 Fare 2.717797 3 SameTicketCnt 3.289298 4 Pclass_str_1 3.105142 5 Pclass_str_3 2.886867 6 Sex_female 2.277466 7 Embarked_Q 1.549674 8 Embarked_S 4.240749
VIFが5以上の変数は無くなりましたので、多重共線性の確認は完了になります。
モデリングをするときは選択して残った上記変数で実施します。
データのエクスポート
学習とテストデータをエクスポートします。
次回から加工済みデータを読み込むことによって欠損値処理と特徴量エンジニアリングの作業を短縮することができます。
学習用データのエクスポート
df.to_csv("titanic_train.csv", index=False)テスト用データのエクスポート
今回作成したdf_testは欠損値を補完するのではなく、除外してしまったので新しく欠損値を推定したデータを作成します。
(テストデータのレコード数がkaggleにアップロードしたときに一致していないとエラーになります。)
# テストデータの加工
df_eval = pd.read_csv("/Users/hinomaruc/Desktop/notebooks/titanic/test.csv")
df_eval['Pclass_str'] = df_eval['Pclass'].apply(str)
df_eval = df_eval.join(pd.DataFrame(enc.transform(df_eval[['Pclass_str','Sex','Embarked']]).toarray(),columns=cols))
df_eval['FamilyCnt'] = df_eval['SibSp'] + df_eval['Parch'] + 1
df_eval["SameTicketCnt"] = df_eval.groupby('Ticket')["Ticket"].transform('count')
FEATURE_COLS=[
'SibSp'
, 'Parch'
, 'Fare'
, 'Pclass_str_1'
, 'Pclass_str_2'
, 'Pclass_str_3'
, 'Sex_female'
, 'Sex_male'
, 'Embarked_C'
, 'Embarked_Q'
, 'Embarked_S'
]
# Ageの推定
df_eval["Age_predicted"] = bestmodel.predict(df_eval[FEATURE_COLS])
df_eval.Age = np.where(df_eval.Age.isnull(), df_eval.Age_predicted, df_eval.Age)
# 不必要カラムの削除
df_eval = df_eval.drop(columns=["Pclass_str","Age_predicted"])# Fareの欠損値を確認
df_eval.loc[df_eval.Fare.isnull()]
PassengerId Pclass Name Sex Age SibSp Parch Ticket Fare Cabin ... Pclass_str_2 Pclass_str_3 Sex_female Sex_male Embarked_C Embarked_Q Embarked_S FamilyCnt SameTicketCnt 152 1044 3 Storey, Mr. Thomas male 60.5 0 0 3701 NaN NaN ... 0.0 1.0 0.0 1.0 0.0 0.0 1.0 1 1 1 rows × 22 columns
Pclass=3の男性のようです。FareをPclass=3の中央値で置換してあげることにします。
# FareをPclass=3の中央値で置換
replace_val = df.loc[df.Pclass == 3].groupby(['Pclass'])['Fare'].median().values[0]
df_eval["Fare"] = df_eval["Fare"].fillna(value = replace_val)# 欠損値の確認
df_eval.loc[df_eval.Fare.isnull()]
PassengerId Pclass Name Sex Age SibSp Parch Ticket Fare Cabin ... Pclass_str_1 Pclass_str_2 Pclass_str_3 Sex_female Sex_male Embarked_C Embarked_Q Embarked_S FamilyCnt SameTicketCnt 0 rows × 21 columns
Fareが欠損していたレコードがなくなりました。
# 欠損の確認
df_eval.info()
RangeIndex: 418 entries, 0 to 417
Data columns (total 21 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 PassengerId 418 non-null int64
1 Pclass 418 non-null int64
2 Name 418 non-null object
3 Sex 418 non-null object
4 Age 418 non-null float64
5 SibSp 418 non-null int64
6 Parch 418 non-null int64
7 Ticket 418 non-null object
8 Fare 418 non-null float64
9 Cabin 91 non-null object
10 Embarked 418 non-null object
11 Pclass_str_1 418 non-null float64
12 Pclass_str_2 418 non-null float64
13 Pclass_str_3 418 non-null float64
14 Sex_female 418 non-null float64
15 Sex_male 418 non-null float64
16 Embarked_C 418 non-null float64
17 Embarked_Q 418 non-null float64
18 Embarked_S 418 non-null float64
19 FamilyCnt 418 non-null int64
20 SameTicketCnt 418 non-null int64
dtypes: float64(10), int64(6), object(5)
memory usage: 68.7+ KB
分析に利用するカラムが「418 non-null」になっていれば問題ありません。
# テストデータのエクスポート
df_eval.to_csv("titanic_eval.csv",index=False)まとめ
データ加工パートも今回で一旦完了です。
次からはとうとうモデリングパートに入ります。
色々なモデルを試して生存有無を予測しKaggleにアップしてみようとかなと思っています。
また、automlも試してみようかなと思っています。
参考
*1
Moderate multicollinearity may not be problematic. However, severe multicollinearity is a problem because it can increase the variance of the coefficient estimates and make the estimates very sensitive to minor changes in the model. The result is that the coefficient estimates are unstable and difficult to interpret. Multicollinearity saps the statistical power of the analysis, can cause the coefficients to switch signs, and makes it more difficult to specify the correct model. 引用:What Are the Effects of Multicollinearity and When Can I Ignore Them?
*2
If two variables are highly correlated, increases in one may be offset by decreases in another so the combined effect is to negate each other. consider the actual impact of multicollinearity. It doesn't change the predictive power of the model 引用: Why is multicollinearity not checked in modern statistics/machine learning
*3
Assume a number of linearly correlated covariates/features present in the data set and Random Forest as the method. Obviously, random selection per node may pick only (or mostly) collinear features which may/will result in a poor split, and this can happen repeatedly, thus negatively affecting the performance.
assume that the features are ranked high in the 'feature importance' list produced by RF. As such they would be kept in the data set unnecessarily increasing the dimensionality.
Should one be concerned about multi-collinearity when using non-linear models?